第七节 圆的方程

切点弦方程

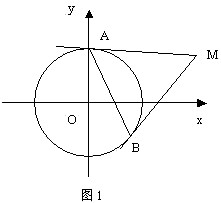
　　问题1：过圆 外一点 ，作这个圆的两条切线 、 ，切点分别是 、 ，求直线 的方程（直线 称作切点弦）．

　　解：如图所示，设切点 的坐标为 ，切点 的坐标为 ．

因为圆的方程是

　　　　　①

所以过圆上一点 所作的切线的方程为

　 　　　②

由于 在直线 上，所以

　　　　③

同理，根据点M在切线BM上，得

　　　　　　④

③④表明，点 和点 都在下面的直线上

⑤

因为过两点只有一条直线，所以⑤就是直线 的方程．

即点 的切点弦方程为： ．

问题1解法的基本思想是设而不求．设了点 和点 的坐标，但是不求出这些坐标，只是借用它们的形式，把最终的问题解决．

从问题1中，我们不仅学习了切点弦方程，还学习了设而不求的解题思想．下面看一个与之相关的问题．

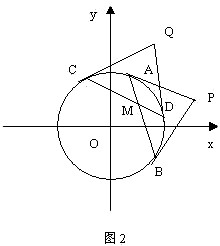
问题2：设 是圆 内的一点，但不是圆心．过点 任意作两条不通过圆心的弦 和 ，分别过点 、 作圆的切线相交于点 ，过点 、 作圆的切线相交于点 ．求直线 的方程．

    解：如图，设点 的坐标为 ，点 的坐标为 ．

因为圆的方程是

　　　　　①

、 是过圆外一点所作圆的切线， 、 是切点，所以切点弦 的方程为

 　　　　　　　②

同理切点弦 的方程为

 　　　　③

因为 在直线 上，所以

 　　④

同理 在直线 上，所以

⑤

④⑤表明点，点 和点 都在下面的直线上

⑥

　　因为过两点只有一条直线，所以⑥就是直线 的方程．

　　不难看出，上述两个问题的紧密联系，同样是用设而不求的思想方法，问题2还运用了问题１的结论，更为有趣的是二者其实还是一个问题的两个方面，具体如下：

一般地，已知圆 和平面内的任意点 ，只要 不是圆心（0，0），总可以作出对应的直线 ．这样得到的直线 叫做点 关于圆的极线（当 在圆外时， 也叫切点弦），点 叫作直线 的极点．

　　问题1　是点 在圆外时的情况，问题2是点 在圆内时的情况，并且同时也给出了作相应极线的几何作图方法．当然，点 在圆上时，它的极线就是过点 的圆的切线．三种情况的极线方程都是 ，这种高度的统一性真是妙不可言．其实极点、极线的概念就是切点、切线概念的推广，它们还有很多重要的性质，高等几何里有详细研究．

圆幂定理

　　问题3：过点 任作直线交定圆于两点 、 ，证明 为定值（圆幂定理）．

　　证：以 为原点，设圆的方程为

  　①

　　过 的直线为

　　则 、 的横坐标是方程

的两个根 、 ．由韦达定理

 　　　　　

于是

圆①也可以写成

①′

　　其中 为圆的半径的平方．所说的定值 也就是 （原点）与圆心 的距离的平方减去半径的平方．当 在圆外时，这就是自 向圆所引切线（长）的平方．

　　这定值称为点 到这圆的幂．

　　在上面证明的过程中，我们以 为原点，这样可以使问题简化．

　　如果给定点 ，未必是原点，要求出 关于圆①的幂（即 ），我们可以设直线 的方程为

　　　　　　　　　　②

　　　　　　　　　　③

 是 的倾斜角， 表示直线上的点与 的距离．

　　将②③代入①得

　　即

， 是它的两个根，所以由韦达定理

　　　　　④

是定值

　　④是 关于①的幂（当 是原点时，这个值就是 ）．它也可以写成

   ④′

　　即 与圆心 距离的平方减去半径的平方．

　　当 在圆内时，幂值是负值； 在圆上时，幂为0； 在圆外时，幂为正值，这时幂就是自 向圆所引切线长的平方．

　　以上是圆幂定理的证明，下面看一看它的应用．

　　问题4：自圆外一点 向圆引割线交圆于 、 两点，又作切线 、 ， 、 为切点， 与 相交于 ，如图．求证 、 、 成调和数列，即

　　证：设圆的方程为

⑤

　　点 的坐标为 ， 的参数方程为

　　　　⑥

 　　　⑦

　　其中 是 的倾斜角， 表示直线上的点 与 的距离．

　　⑥⑦代入⑤得

　　即

    　　　　　　

 、 是它的两个根，由韦达定理

　　　⑧

　　另一方面，直线 是圆的切点弦，利用前边的结论， 的方程为

　　⑦⑧代入得

　　因此，这个方程的根 满足

　　　⑨

　　综合⑧⑨，结论成立．

　　可以证明，当 在园内时，上述推导及结论仍然成立．

　　说明：问题4的解决借用了问题3的方法，同时我们也看到了问题4与问题1、问题2的内在联系．