第四节 双曲线的几何性质

扩展资料

“姊妹”双曲线辨析

下面的四条双曲线，其方程形式相象：

（1）；　　 （2）；

（3）； （4）

性质又相近，我们称之为“姊妹”双曲线．她们的关系如何呢？让我们辨析一下吧．

　　先看（1）与（2），把方程（1）右边的1换成－1，就可得到（2）．这里，一条双曲线的实轴是另一条双曲线的虚轴，称为共轭双曲线．

　　再看（1）与（3），把方程（1）中 、 互换，就可得到（3），所以，这两条双曲线关于直线 对称．实际上，双曲线（3）可以看作是将双曲线（1）绕着原点旋转90°而得到的，故称为转置双曲线．

　　最后看（1）与（4）．把方程（1）中 、 互换，就可得到（4）．也可以这样进行：把方程（1）中 、 互换，又把方程（1）右边的1换成－1，就能得到（4）．因此，双曲线（4）可以看成是把双曲线（1）的共轭双曲线（即（2））转置90°而得到的，故称为共轭转置双曲线．

　　至此，“姊妹”双曲线的关系已经明了．

                              ；

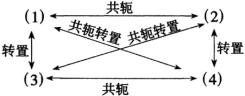
　　那么，“姊妹”双曲线的性质如何呢？请看下表，就一目了然了：

　　有没有一种双曲线，它的共轭双曲线就是转置双曲线呢？有的！这就是等轴双曲线．

返回

扩展资料

双曲线中点弦存在性的探讨

求过定点的双曲线的中点弦问题，通常有下面两种方法：

　　（1）点差法，即设出弦的两端点的坐标代入双曲线方程后相减，得到弦中点坐标与弦所在直线斜率的关系，从而求出直线方程．

　　（2）联立法，即将直线方程与双曲线方程联立，利用韦达定理与判别式求解．

　　无论使用点差法还是联立法，都要运用 来判定中点弦是否存在，而这完全取决于定点所在的区域．现分析如下：

　　利用双曲线及其渐近线，可把平面分成Ⅰ、Ⅱ、Ⅲ三个区域（如图）．

　　当 在区域Ⅰ内时，有 ．

　　当 在区域Ⅱ内时，有 ．

　　当 在区域Ⅲ内时，有 ．

　　利用上述结论，可以证明：

　　当 在区域Ⅰ时，以它为中点的弦不存在，而在区域Ⅱ、Ⅲ时，这样的弦是存在的．证明过程如下：

　　设双曲线 的弦 两端点为 ， ，中点为 ，则 ， ．

　　运用点差法得出 的斜率 ．            ①

　　令直线 的方程为 ，

　　即         ．               ②

　　把②代入 ，整理得

 ．



   ．               ③

　　把①代入③，整理得 ．

　　若 在Ⅱ、Ⅲ区域内，则 或 ，这时 ，中点弦存在；

　　若 在区域Ⅰ内，则 ，这时 ，中点弦不存在．

　　例  过点 作双曲线 的弦 ，使 点为 的中点，则 的方程为（      ）

　　（A） （B）

　　（C） （D）不存在

　　分析  将 及 联立得 ．此时， ，则选（D）．

　　若运用上述区域法，只要判断 在区域Ⅰ就可得出中点弦不存在的结论，故可直接选（D）．

返回