 设为首页
设为首页
 加入收藏
加入收藏
关于球的考查分类及其对策
高考中时常出现与球有关的题目的考查,这类题目具有一定的难度.考试说明中对这类题目有如下要求:掌握球的表面积和体积公式,解决与球的截面有关的问题.这就是这类题目既有可能考查,但又不作过难考查.故题目的考查多出现在选择题、填空题中.因此要想解决好球的问题,必须心中有数,明确大纲要求,防止复习方向出现偏差,下面就这类问题的考查分类及解决对策谈一些看法.
一、考查与球相切的问题
球的相切问题比较容易解决,关键是抓住相切时的实质,即切点到球心的距离等于其半径.
例1 设正方体的全面积为![]() ,一个球内切于此正方体,那么这个球的体积是(
)
,一个球内切于此正方体,那么这个球的体积是(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
分析 设正方体的棱长为![]() ,球的半径为
,球的半径为![]() ,则
,则![]() ,又
,又![]() ,故
,故![]() .
.
∴![]() ,故选(B)
,故选(B)
例2 已知轴截面是正方形的圆柱与球的直径相等,则圆柱的全面积与球的表面积之比是( )
(A)6:5 (B)5:4 (C)4:3 (D)3:2
分析 这里实质上是球内切于一个圆柱.设球的半径为![]() ,则
,则![]() ,
,![]() ,得
,得![]() ,故选(D).
,故选(D).
二、考查球的内接问题
把一个多面体的几个顶点放在球面上,或把一个旋转体的顶点及底面放在球面上来考查有关问题,即球的内接问题.解决这类问题的关键是抓住内接的特点(即球心到多面体的顶点的距离等于球的半径,或旋转体的轴截面是平面图形).发挥好空间想象力,借助于数形结合进行转化,问题即可得解.
例3
已知圆台上、下底面圆周都在球面上,且下底面通过球心,母线与底面所成的角为![]() ,则圆台的体积与球的体积之比为_____________.
,则圆台的体积与球的体积之比为_____________.
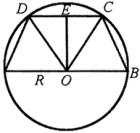
分析 如图,这是圆台和球![]() 的截面图.设圆台的轴截面为
的截面图.设圆台的轴截面为![]() ,球的半径为
,球的半径为![]() ,由已知可得
,由已知可得![]() ,
,![]() ,故
,故![]() .所以
.所以![]() .过
.过![]() 作
作![]() 于
于![]() ,则
,则![]() .
.
∴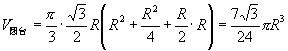 ,
,
![]() .
.
∴ ![]() .
.
例4 长方体的一个顶点上三条核的长分别是3,4,5,且它的八个顶点都在同一个球面上,则这个球的表面积是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
分析 设球的半径为![]() ,则由已知得
,则由已知得![]() ,故
,故![]() .于是
.于是![]() .故选(C).
.故选(C).
注 这类问题有时根据图的特殊性,可利用补图法妙解.
三、考查球面上的点与球的关系
这类问题多是通过球面上的三点(由于不共线)得到一个小圆,再利用小圆的特殊性达到考查球的半径、面积、体积之目的.解决这类问题关键是抓住小圆上的点(即球面上的点)到球心的距离等于半径及公式![]() (
(![]() 为小圆圆心到球心的距离,
为小圆圆心到球心的距离,![]() 为球的半径,
为球的半径,![]() 为小圆的半径).
为小圆的半径).
例5 已知球面上![]() ,
,![]() ,
,![]() 三点的截面到球心的距离等于球的半径的一半,且
三点的截面到球心的距离等于球的半径的一半,且![]() ,则球的面积是(
)
,则球的面积是(
)

(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
分析 如图,设过![]() ,
,![]() ,
,![]() 三点的截面小圆与球的半径分别为
三点的截面小圆与球的半径分别为![]() ,
,![]() ,截面圆心、球心分别为
,截面圆心、球心分别为![]() 、
、![]() .由已知,得
.由已知,得![]() ,
,![]() ,
,![]() .由
.由![]() ,得
,得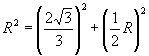 .故选(D).
.故选(D).
扩展资料
计算球面距离的三种习题示范
现行课本中,介绍了球面距离的概念,这方面的习题很多,同学们学习时普遍感到困难.下面给出这类习题解答的示范,以供同学们参考.
1.位于同一纬度线上两点的球面距离
例1 已知![]() ,
,![]() 两地都位于北纬
两地都位于北纬![]() ,又分别位于东经
,又分别位于东经![]() 和
和![]() ,设地球半径为
,设地球半径为![]() ,求
,求![]() ,
,![]() 的球面距离.
的球面距离.
分析:要求两点![]() ,
,![]() 的球面距离,过
的球面距离,过![]() ,
,![]() 作大圆,根据弧长公式,关键要求圆心角
作大圆,根据弧长公式,关键要求圆心角![]() 的大小(见图1),而要求
的大小(见图1),而要求![]() 往往首先要求弦
往往首先要求弦![]() 的长,即要求两点的球面距离,往往要先求这两点的直线距离.
的长,即要求两点的球面距离,往往要先求这两点的直线距离.
解 作出直观图(见图2),设![]() 为球心,
为球心,![]() 为北纬
为北纬![]() 圈的圆心,连结
圈的圆心,连结![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .由于地轴
.由于地轴![]() 平面
平面![]() .
.
∴![]() 与
与![]() 为纬度
为纬度![]() ,
,![]() 为二面角
为二面角![]() 的平面角.
的平面角.
∴![]() (经度差).
(经度差).
![]() △
△![]() 中,
中,![]() .
.

△![]() 中,由余弦定理,
中,由余弦定理,
![]()
 .
.
△![]() 中,由余弦定理:
中,由余弦定理:
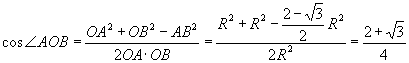 ,
,
∴![]() .
.
∴![]() 的球面距离约为
的球面距离约为![]() .
.
2.位于同一经线上两点的球面距离
例2 求东经![]() 线上,纬度分别为北纬
线上,纬度分别为北纬![]() 和
和![]() 的两地
的两地![]() ,
,![]() 的球面距离.(设地球半径为
的球面距离.(设地球半径为![]() ).(见图3)
).(见图3)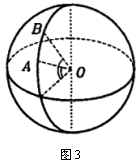
解 经过![]() 两地的大圆就是已知经线.
两地的大圆就是已知经线.
![]() ,
,![]() .
.
3.位于不同经线,不同纬线上两点的球面距离
例3 ![]() 地位于北纬
地位于北纬![]() ,东经
,东经![]() ,
,![]() 地位于北纬
地位于北纬![]() ,东经
,东经![]() ,求
,求![]() ,
,![]() 两地之间的球面距离.(见图4)
两地之间的球面距离.(见图4)
解 设![]() 为球心,
为球心,![]() ,
,![]() 分别为北纬
分别为北纬![]() 和北纬
和北纬![]() 圈的圆心,连结
圈的圆心,连结![]() ,
,![]() ,
,![]() .
.
![]() △
△![]() 中,由纬度为
中,由纬度为![]() 知
知![]() ,
,
∴![]() ,
,
![]() .
.
![]() △
△![]() 中,
中,![]() ,
,
∴![]() ,
,![]()
∴![]() .
.
注意到![]() 与
与![]() 是异面直线,它们的公垂线为
是异面直线,它们的公垂线为![]() ,所成的角为经度差
,所成的角为经度差![]() ,利用异面直线上两点间的距离公式.
,利用异面直线上两点间的距离公式.
![]() (
(![]() 为经度差)
为经度差)

![]() .
.
△![]() 中,
中,![]()

![]() .
.
∴![]() .
.
∴![]() 的球面距离约为
的球面距离约为![]() .
.
扩展资料
球面距离的计算及其计算公式
在球面上,不在同一直径上的两点之间的最短距离,就是经过这两点的大圆在这两点间的一段劣派的长度,我们把这段抓长叫做球面上这两点间的球面距离.(也叫球面上的短程线或测地线)
如图1,A、B为球面上不在同一直径上的两点,![]() 为圆心,⊙
为圆心,⊙![]() 为过A、B的大圆,⊙
为过A、B的大圆,⊙![]() 为过A、B的任一个小圆,我们把这两个圆画在同一个平面内.(见图2)设
为过A、B的任一个小圆,我们把这两个圆画在同一个平面内.(见图2)设![]() ,
,![]() ,球半径为
,球半径为![]() ,半径为
,半径为![]() .则有
.则有![]() 大圆弧长
大圆弧长![]() ,
,![]() 小圆弧长
小圆弧长![]()
![]() (1)
(1)
但![]() ,即
,即
![]() (2)
(2)
将(2)代入(1)得
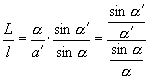 (3)
(3)

∵ ![]() ,由(2)式知
,由(2)式知![]() .
.
由于![]() ,故只需证明函数
,故只需证明函数![]() 在
在![]() 内为单调递减即可.
内为单调递减即可.
∴ ![]()
(∵当![]() 时,有
时,有![]() )
)
∴ ![]() 在
在![]() 单调递减
单调递减
由(3)式不难得到
![]()
即![]() . 故大圆劣弧最短。
. 故大圆劣弧最短。
球面距离公式:设一个球面的半径为![]() ,球面上有两点
,球面上有两点![]() 、
、![]() . 其中
. 其中![]() ,
,![]() 为点的经度数,
为点的经度数,![]() 、
、![]() 为点的纬度数,过
为点的纬度数,过![]() 、
、![]() 两点的大圆劣弧所对的圆心角为
两点的大圆劣弧所对的圆心角为![]() ,则有
,则有
![]() (弧度)
(弧度)
A、B间的球面距离为:
![]()
证明:如图3,⊙![]() 与⊙
与⊙![]() 分别为过A、B的纬度圈,过A、C的大圆,过
分别为过A、B的纬度圈,过A、C的大圆,过![]() 、D的大圆分别为A、B的经度圈,而经度圈与纬度圈所在的平面互相垂直,作
、D的大圆分别为A、B的经度圈,而经度圈与纬度圈所在的平面互相垂直,作![]() 面
面![]() ,垂足
,垂足![]() 位于
位于![]() 上,连结
上,连结![]() 、
、![]() . 则
. 则
![]()
![]()
![]()
在![]() 中,由余弦定理,得:
中,由余弦定理,得:
![]()
![]()
![]()
![]()
故![]()
又![]()
比较上述两式,化简整理得:
![]()
从而可证得关于![]() 与
与![]() 的两个式子.
的两个式子.
例题 北京在东经![]() ,北纬
,北纬![]() ,上海在东经
,上海在东经![]() ,北纬
,北纬![]() ,求北京到上海的球面距离.
,求北京到上海的球面距离.
解:![]()
![]()
∴ ![]() (弧度)
(弧度)
∴ 所求球面距离为
![]()