 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
杨辉
 杨辉,中国南宋时期杰出的数学家和数学教育家。在13世纪中叶活动于苏杭一带,其著作甚多。
杨辉,中国南宋时期杰出的数学家和数学教育家。在13世纪中叶活动于苏杭一带,其著作甚多。
他著名的数学书共五种二十一卷。著有《详解九章算法》十二卷(1261年)、《日用算法》二卷(1262年)、《乘除通变本末》三卷(1274年)、《田亩比类乘除算法》二卷(1275年)、《续古摘奇算法》二卷(1275年)。
 杨辉的数学研究与教育工作的重点是在计算技术方面,他对筹算乘除捷算法进行总结和发展,有的还编成了歌决,如九归口决。
杨辉的数学研究与教育工作的重点是在计算技术方面,他对筹算乘除捷算法进行总结和发展,有的还编成了歌决,如九归口决。
他在《续古摘奇算法》中介绍了各种形式的“纵横图”及有关的构造方法,同时“垛积术”是杨辉继沈括“隙积术”后, 关于高阶等差级数的研究。杨辉在“纂类”中,将《九章算术》246个题目按解题方法由浅入深的顺序,重新分为乘除、分率、合率、互换、二衰分、叠积、盈不足、方程、勾股等九类。 我们将在二项式定理的学习中,接触到杨辉三角。
扩展资料
杨辉的数学和教育普及工作
杨辉,字谦光,南宋末钱塘人(今杭州市),曾作过地方官员.陈几先为他的《日用算法》一书写跋时,赞他“以廉饬已,以儒
![]() 吏;吐胸中之灵气,继前贤之奥旨.”他是宋代甚至也是中国古代最杰出的数学教育家,十分重视数学的教育和普及工作.他在1261年到1275年间先后完成数学著作五种二十一卷.计有《详解九章算法》及附《九章算法篡类》共十二卷(1261年)、《日用算法》二卷(1262年)、《乘除变通本末》三卷(1274年)、《田亩比类乘除捷法》二卷和《续古摘奇算法》二卷(1275年).他编写的这几种书内容大都较浅显,适合于教学之用或作普及读本.
吏;吐胸中之灵气,继前贤之奥旨.”他是宋代甚至也是中国古代最杰出的数学教育家,十分重视数学的教育和普及工作.他在1261年到1275年间先后完成数学著作五种二十一卷.计有《详解九章算法》及附《九章算法篡类》共十二卷(1261年)、《日用算法》二卷(1262年)、《乘除变通本末》三卷(1274年)、《田亩比类乘除捷法》二卷和《续古摘奇算法》二卷(1275年).他编写的这几种书内容大都较浅显,适合于教学之用或作普及读本.
杨辉在《详解九章算法》自序中说,“《九章》为算经之首”,所以“尊尚此书,留意详解.”贾宪著《黄帝九章算法细草》是为刘徽注的《九章》撰演细草,杨辉又对贾宪的《细草》作了详解,谓之“恐问隐而添题解,见法隐而续释注,刊大小字以明法草,增比类题以通俗务,凡题法解白不明者别图而验之.”
他的著作的特点是图文并茂,并授编了许多歌诀,以便于学习和理解.如在《详解》书首,他补画了一卷图形,“列图于卷首”,可惜原图散失了.他对许多问题都配画了插图,有些图画得很生动,例如《九章》“勾股章”第九题“圆材理壁中,以锯锯之”,他配画了锯子锯圆材的逼真图形;“勾股章”第十九题,“今有邑,方不知大小”,他形象地画出了方邑和北门三十步外的一棵树等等.这些在今天初级课本中的做法在古代的数学书中是很少见的.
他还第一次突破了《九章》的传统分类,按“因法推类”的原则,重新进行了《篡类》.即按算法将《九章》的题目重新分成乘除、互换、合率、分率、衰分、迭积、盈不足、方程、勾股九类,并给出相应的题目.这是历代诸多对《九章》作过注释的书所没有的创举.
杨辉的《详解》还在《九章》的知识内容的基础上有所发展.比如对“商功章”的多面体,他以各种堆垛相类比,在沈括“隙积术”的基础上,又提出了几种堆垛的求积问题,如(用现代符号表示)
(1)方垛

(2)果子垛
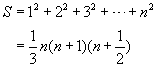
(3)三角垛

(4)果子垛

![]()
其中(4)式与沈括的“隙积木”是相同的.其余各式都是(4)式的特例.杨辉把这些级数求和公式都用文字来表述.如(2)式的垛积为“下方加一,乘下方,为平积,又加半为高以乘下方,为高积,如三而一.”
杨辉还做了大量简化算法的工作.比如在《乘除通变本末》中,他系统地叙述了唐宋相传的以加代乘,以减代除的方法.他对“求——乘”和“求——除”还编拟了歌诀,朗朗上口,很便记忆.“求——乘”的口诀是
五六七八九,倍之数不走,
二三须当半,遇四两折扭.
倍折本从法,实即反其有,
用加以代乘,斯数足可守.
“求——除”的口诀将上面的后四句改为
培折本从法,为除积相就,
用减以代除,定位求如旧.
比如计算“法”56乘“实”237.由第一句应将56“倍之”得112,由第二句将237“折半”为118.5,于是对237×56实际变为118.5×(100+10+2)=11850+1185-237=13272.因为筹算加法简便得多,所以这种方法在当时是有意义的.其他的歌诀和口诀还有很多,包括一些已经失传的.这些都表现了杨辉传播和普及数学的良苦用心.
在《乘除通变本末》上卷有一篇“习算纲目”,可以说是杨辉普及数学教育的经验总结.开头就提出,“先念九九合数”,主张应“由一一如一至九九八十一”,“从小至大”学口诀.过去的九九表是由九九八十一开头的,不符合学习规律.自南宋以后,九九口诀表就改正过来了.杨辉的“习并纲目”是一份很有价值的数学教学计划和教学法纲要,他主张按内容难易循序渐进地学习,温故而知新,在新内容学习之后都安排了复习.特别强调学习要明算理,要“讨论用法之源”.还对所学的内容指定了参考书籍等等.
除此以外,杨辉还进行过一些理论研究.特别是对纵横图(幻方)的研究,有创造性成果.自汉代“九宫图”以来人们对其数字结构赋予了一种神秘色彩,甚至认为是天生的神赐——洛书.杨辉对纵横图的构成规律进行了深入的研究,在他的《续古摘奇算法》书中,就记载了将近二十个纵横图.除方形图以外,还有其他形状排列的,最大的“百子图”已是由1至100的数排成的十阶纵横图(如图所示),纵横之和均为505;另外还有圆形的“攒九图”,由1到33排成四个同心圆,中间是9,四条直径上的数之和为147,各圆周上的数之和为138.他的纵横图对后世有很大影响,此后对纵横图的研究一直持续不断.
| 1 |
20 |
21 |
40 |
41 |
60 |
61 |
80 |
81 |
100 |
| 90 |
82 |
79 |
62 |
59 |
42 |
39 |
22 |
19 |
2 |
| 3 |
18 |
23 |
38 |
43 |
58 |
63 |
78 |
83 |
98 |
| 97 |
84 |
77 |
64 |
57 |
44 |
37 |
24 |
17 |
4 |
| 5 |
16 |
25 |
36 |
45 |
56 |
65 |
76 |
85 |
96 |
| 95 |
86 |
75 |
66 |
55 |
46 |
35 |
26 |
15 |
6 |
| 14 |
7 |
34 |
27 |
54 |
47 |
74 |
67 |
94 |
87 |
| 88 |
93 |
68 |
73 |
48 |
53 |
28 |
33 |
8 |
13 |
| 12 |
9 |
32 |
29 |
52 |
49 |
72 |
69 |
92 |
80 |
| 91 |
90 |
71 |
70 |
51 |
50 |
31 |
30 |
11 |
10 |
扩展资料
帕斯卡
帕斯卡(Blaise Pascal,1623~1662)法国数学家、物理学家、哲学家,1623年出生于克莱蒙费朗,后迁居巴黎。父亲是著名的数学家。他从小学习优异,善于思考,对数学和物理特别爱好,人称为神童。16岁就参加了巴黎的数学与物理学界的学术活动,并发表第一篇论文《圆锥曲线论》,提出的定理成为后来投影几何的基本定理之一(“圆锥曲线内接六边形的三对边交点共线“)。在大家听了他的当面论述后,才相信该论文不是他父亲代劳的。18岁时他创制了第一架机械式计算器。曾发表过一些有关算术级数和二项式系数的论文,例如在《论算术三角形》的论文中提出二项式系数的三角形排列法(这一三角形已由我国杨辉早在 1261年《详解九章算法》中得出)。他还是概率论的创始人之一。
他在物理学上的主要贡献是对大气压强和流体静力学的研究。当托里拆利1643年的真空实验传到法国后,帕斯卡在 1646年重复其实验获得成功(需要有优质玻璃管)。他还把12米长的玻璃管固定在船的桅杆上用水和葡萄酒做托里拆利实验。人们原以为葡萄酒中含有“气”元素,因此酒柱会比水柱短。但因为酒的密度比水小,结果酒柱比水柱还要高。1647年他发表了《关于真空的新实验》一书。1646~1651年他还在巴黎、多姆山等地的多次试验中证实了大气压强随高度的增加而减小,并与当地气象条件有关,从而预示了利用气压计预报气象的前景。
帕斯卡还从力的平衡的观点进一步研究了流体的平衡。他说山顶气压计实验“使我亲眼看到了自然界中最轻的流体空气和最重的流体水银之间的平衡”。
在他逝世后第二年(1663)出版的《论液体平衡和空气的重量》中,分别论述了流体静力学和气体力学,书中提出了帕斯卡定律。他把封闭容器中每一部分都比作一部机器,其中各力的平衡,就像杠杆和其他简单机械一样,遵循着同样规律。他在这本书中曾写道:“使一百磅水移动一英寸,与使一磅水移动一百英寸显然是一回事”,从而提出了水压机的原理。他还详细证明了器壁上由于液重产生的压强仅与深度有关,从理论上解释了流体静力学佯谬。更可贵的是,他把实验作为科学推论的一个有机环节,强调在自然科学中实验才是唯一可以信赖的良师,用以批驳耶稣教会神父反对真空存在的论点。大气压强单位就是用帕斯卡命名的。
他从18岁起身体开始衰弱,以后一直疾病缠身,又由于父丧和一次突发的马车事故,打断了他在科学事业中的创造性才华。31岁时,他重新接受洗礼,后退隐于修道院,转而在神学、哲学(《思想录》,1670发表)上写作,1662年8月19日病逝于巴黎,终年39岁。
扩展资料
帕斯卡三角形
右图是在棋盘格上 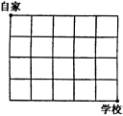 做成的行走路线.西北角是某人自己的家,东南角是学校,问从自己家经东西5条街南北4条街到学校(最短距离)有几种走法?
做成的行走路线.西北角是某人自己的家,东南角是学校,问从自己家经东西5条街南北4条街到学校(最短距离)有几种走法?
向东走一格写一个E,向南走一个格写一个S,例如沿着左图的粗线走,表示为::EESESSEES.
 于是将E和S合起来9条通路中,选择四次S即可,所以通路的,总数可以考虑为
于是将E和S合起来9条通路中,选择四次S即可,所以通路的,总数可以考虑为
![]() 条.
条.
这个问题到此已全部解决了.可是对于计算
![]() 不熟悉的人来说,如用下图交叉点处的圆表示,在圆中写上“到此为止行走的道路条数”.回答为126条,一看图形你就会立即明白了.
不熟悉的人来说,如用下图交叉点处的圆表示,在圆中写上“到此为止行走的道路条数”.回答为126条,一看图形你就会立即明白了.

这个图在什么地方应见过,你还记得吗?它被称为“帕斯卡三角形”。用斜线连接的数的排列实际上正是
![]() 展开时出现的系数。
展开时出现的系数。

扩展资料
神龟龙马,洛书河图
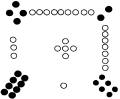 公元前2200年,我国商周时代的《易经》中载:大禹治伏水患之后,洛河上浮出一只巨型神龟,背驮如图所示的“洛书”献给大禹,作为苍天对他治水有功造福百姓的奖励.这幅天书横看竖看和斜看,每一组由黑点子●与白点子○合成,总点数皆为15.后来人们把此洛书翻译成如图所示的一个所谓幻方.
公元前2200年,我国商周时代的《易经》中载:大禹治伏水患之后,洛河上浮出一只巨型神龟,背驮如图所示的“洛书”献给大禹,作为苍天对他治水有功造福百姓的奖励.这幅天书横看竖看和斜看,每一组由黑点子●与白点子○合成,总点数皆为15.后来人们把此洛书翻译成如图所示的一个所谓幻方.

所谓幻方,是由1,2,3,…,
![]() ,
, ![]() 组成的一个数字方阵,每数恰在此阵中出现一次,且每行之和,每列之和和两条对角线上的数字之和皆相等.
组成的一个数字方阵,每数恰在此阵中出现一次,且每行之和,每列之和和两条对角线上的数字之和皆相等.
1275年,我国宋代著名数学家杨辉把洛书形象地描写为:“九子斜排,上下对易,左右相更,四维挺进,戴九履一,左三右七,二四为肩,六八为足.”破译了洛书的玄机,见图.

“九子斜排”是按箭头方向分别把1,2,3,4,5,6和7,8,9排成具有右下方走向的一排,三个斜排组成一个倾斜45°角的正方形阵.
“上下对易”,指1与9对换,1移入最下空格,9移入最上空格,使得正中的头部戴了一个9的帽子,正中最低处穿了一双1字鞋,即“戴九履一”.
“左右相更”,指最右边的3与最左边的7对调,3移至左侧空格,7移至右侧空格.
至此造成一个四方阵,即“四维挺进”,又2与4分别在右上角(肩)与左上角,6与8分别在右下角(足)与左下角,即“二四为肩”“六八为足”.
杨辉的这种口诀中的关键词是“
![]() 子斜排”“四维挺进”“上下对易”和“左右相更”四句.下面两图分别给出按杨辉口诀构作的5阶幻方和7阶幻方,任意奇数(大于3)阶的幻方皆可照此制作,但同阶幻方不是唯一的,高阶幻方的个数非常之巨大,例如五阶幻方就有1千多万个!另外,杨辉口诀不适用于偶阶幻方,偶阶幻方的构作十分困难.
子斜排”“四维挺进”“上下对易”和“左右相更”四句.下面两图分别给出按杨辉口诀构作的5阶幻方和7阶幻方,任意奇数(大于3)阶的幻方皆可照此制作,但同阶幻方不是唯一的,高阶幻方的个数非常之巨大,例如五阶幻方就有1千多万个!另外,杨辉口诀不适用于偶阶幻方,偶阶幻方的构作十分困难.


“对易”和“相更”时,移动的步数恰为幻方的阶数,例如上图(a)中顶上的1下降7步至33的上方邻格内,上图(a)中的9下降7步至33的下方邻格内,上图(a)中的7左移7步至25的左侧邻格等等.
洛书对应的幻方史称“神农幻方”.
《易经》上又云,为奖励大禹功绩,一匹龙马从黄河跃出,把如下图所示的一张“河图”赠与大禹.
下图(b)是相应位置上“点子”的个数,不过4个10的意思是被虚线连络的10个黑点子视为分布在它们形成的正方形的四个顶处.这样,河图的数学含量就大了:

从中心5向右加上4等于最右端的9;
从中心5向左加上3等于最左端的8;
从中心5向上加上2等于最上端的7;
从中心5向下加上1等于最下端的6.
斜着看,7+9=2+10+4=16,8+6=3+10+1=14,9+6=4+10+1=15,8+7=2+10+3=15.
洛书和河图出自四千多年前中华民族之手,是世界组合数学的最早成果,值得我们自豪;可惜它被后人神化,未能发展成系统的理论;中国几千年的封建君主统治,鼓励乃至强迫知识分子为皇帝歌功颂德,使大多数知识分子成为什么科学知识也没有只会呼喊皇帝万岁的奴才,在这种社会背景之下,中国的许多本应领先的数学分支和组合数学一样,并没有发展起来.事实上,组合数学不仅是数学科学的重要分支,而且是信息产业和计算机科学的数学基础之一,现代数学教育和数学科研当中,必须给以足够的重视.