第四节 复数的加法与减法

曲线方程的复数形式

　　利用复数形式也可以表示某些点的集合或某些曲线，于是通过复平面把复数与平面解析几何的某些曲线联系起来，而且用复数形式表示曲线方程显得更简单、清晰。

　　用复数形式表达复平面上两点间的距离：

　　设 。

　　则分别表示复数 、 的两点 、 之间的距离为

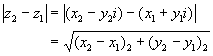
　　若设动点Z，定点 、 、 分别表示复数 、 、 、 ，几种常见曲线的复数形式方程如下：

　　（1）圆： ，其中 为半径， 为圆心对应的复数，单位圆： 。

　　（2）开圆域： 。

　　（3）半开圆环域： ，其中 为内半径， 为外半径，左边等号成立，包括内圆周；右边等号不成立，不包括外圆周。

　　（4）线段的垂直平分线： ，其中 、 为线段的两个端点对应的复数。

　　（5）椭圆： ，其中 、 为对应椭圆的焦点， 为其长轴长。

　　（6）双曲线： ，

其中 、 为双曲线的焦点对应的两个数， 为其实轴的长。

　　（7）抛物线： ，其中 为在 轴正半轴上的焦点所对应的复数 ，定直线与 轴垂直，垂足在 轴的负半轴上，且原点到垂足的距离等于原点到焦点的距离， 的实部是 。

　　这样就把复数问题与解析几何问题联系起来了。某些复数问题可化为解析几何问题，同样某些解析几何问题也可以化为复数问题来解决。