 设为首页
设为首页
 加入收藏
加入收藏
【教学目标】
(1)知道时间和时刻的含义及区别,知道在实验中测量时间的方法;
(2)掌握位移的概念,它是表示质点位置变动的物理量,是矢量,可以用有向线段来表示;
(3)知道路程和位移的区别;
(4)知道直线运动的位置和位移的关系。
【教学重点】
时间和时刻的概念和区别;位移的矢量性、概念。
【教学难点】
位移和路程的区别。
【教学过程】
第二节 时间和位移
1、时刻和时间间隔
(1)时刻和时间间隔可以在时间轴上表示出来。时间轴上的每一点都表示一个不同的时刻,时间轴上一段线段表示的是一段时间间隔(画出一个时间轴加以说明)。
(2)在学校实验室里常用秒表,电磁打点计时器或频闪照相的方法测量时间。
例1:下列说法中指的是时间的有ACEF,指的是时刻的有BDG。
A.第5秒内 B.第6秒初 C.前2秒内 D.3秒末 E.最后一秒内 F.第三个2秒 G.第五个1秒的时间中点。
![]()
课堂训练:
(1)关于时间和时刻,下列说法正确的是(D)
A.物体在5s时就是指物体在5s末时,指的是时刻
B.物体在5s时就是指物体在5s初时,指的是时刻
C.物体在5s内就是指物体在4s末到5s末的这1s时间
D.物体在第5s内就是指物体在4s末到5s末的这1s的时间
2、路程和位移
(1)路程:质点实际运动轨迹的长度,它只有大小没有方向,是标量。
(2)位移:是表示质点位置变动的物理量,有大小和方向,是矢量。它是用一条自初始位置指向末位置的有向线段来表示,位移的大小等于质点始、末位置间的距离,位移的方向由初位置指向末位置,位移只取决于初、末位置,与运动路径无关。
(3)位移和路程的区别:
(4)一般来说,位移的大小不等于路程。只有质点做方向不变的无往返的直线运动时位移大小才等于路程。
例2:中学的垒球场的内场是一个边长为16.77m的正方形,在它的四个角分别设本垒和一、二、三垒.一位球员击球后,由本垒经一垒、一垒二垒跑到三垒,他运动的路程是多大?位移是多大?位移的方向如何?
课堂训练:
(1)以下说法中正确的是(B)
A.两个物体通过的路程相同,则它们的位移的大小也一定相同
B.两个物体通过的路程不相同,但位移的大小和方向可能相同
C.一个物体在某一运动中,位移大小可能大于所通过的路程
D.若物体做直线运动,位移的大小就等于路程
(2)如图甲,一根细长的弹簧系着一个小球,放在光滑的桌面上,手握小球把弹簧拉长,放手后小球便左右来回运动,B为小球向右到达的最远位置,小球向右经过中间位置O时开始计时,其经过各点的时刻如图乙所示。若测得OA=OC=7cm,AB=3cm,则自0时刻开始:
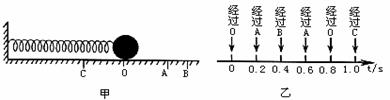
A.0.2s内小球发生的位移大小是7cm,方向向右,经过的路程是7cm
B.0.6s内小球发生的位移大小是7cm,方向向右,经过的路程是13cm
C.0.8s 内小球发生的位移是0,经过的路程是20cm
D.1.0s内小球发生的位移大小是7cm,方向向左,经过的路程是27cm
(3)关于质点运动的位移和路程,下列说法正确的是(AB)
A.质点的位移是从初位置指向末位置的有向线段,是矢量
B.路程就是质点运动时实际轨迹的长度,是标量
C.任何质点只要做直线运动,其位移的大小就和路程相等
D.位移是矢量,而路程是标量,因而位移不可能和路程相等
(4)下列关于路程和位移的说法,正确的是(C)
A.位移就是路程
B.位移的大小永远不等于路程
C.若物体作单一方向的直线运动,位移的大小就等于路程
D.位移是矢量,有大小而无方向,路程是标量,既有大小,也有方向
(5)关于质点的位移和路程,下列说法正确的是(D)
A.位移是矢量,位移的方向就是质点运动的方向
B.路程是标量,也是位移的大小
C.质点做直线运动时,路程等于其位移的大小
D.位移的数值一定不会比路程大
(6)下列关于位移和路程的说法,正确的是(C)
A.位移和路程的大小总相等,但位移是矢量,路程是标量
B.位移描述的是直线运动,路程描述的是曲线运动
C.位移取决于始、末位置,路程取决于实际运动路径
D.运动物体的路程总大于位移
3、矢量和标量
(1)矢量:既有大小、又有方向的物理量。
(2)标量:只有大小,没有方向的物理量。
4、直线运动的位置和位移:在直线运动中,两点的位置坐标之差值就表示物体的位移。
阅读材料:
我国古代关于运动的知识
我国在先秦的时候,对于运动就有热烈的争论,是战国时期百家争鸣的一个题目。《庄子》书上记载着,公孙龙曾提出一个奇怪的说法,叫做“飞鸟之影未尝动也。”按常识说,鸟在空中飞,投到地上的影当然跟着鸟的移动而移动,但公孙龙却说鸟影并没有动,无独有偶,当时还有人提出“镞矢之疾;有不行不止之时”,一支飞速而过的箭,哪能“不行不止”呢?既说“不行”,又怎能“不止”呢?乍看起来,这些说法实在是“无稽之谈”,也可以给它们戴一顶“诡辩”的帽子。
但是事情并不这么简单。这个说法不但不是诡辩,而且还包含着辩证法的正确思想,恩格斯曾经指出,“运动本身就是矛盾,甚至简单的机械的位移之所以能够实现,也只是因为物体在同一瞬间既在一个地方又在另一个地方,既在同一个地方又不在同一个地方,这种矛盾的连续产生和同时解决正好就是运动。”因为运动体的位置随时间而变化,某一时刻在A点,在随之而来的另一时刻,就在相邻的B点,因此,也就有一个时刻,它既在A点又不在A点,既在B点又不在B点,在这时刻,物体岂不是“不行不止”吗?再者,在一定的时间Δt内,物体前进一段距离Δs,当这时间变小,Δs随之变小;当Δt趋近于零时,Δs也趋近于零。也就是说,在某一瞬间,即某一时刻,运动体可以看作是静止的,所以飞鸟之影确实有“未尝动”的时候,对于运动的这种观察和分析实在是十分深刻的,这同他们能够区分“时间”与“时刻”的观念很有关系。《墨经》对于“鸟影”问题又有他们自己的理解,说那原因在于“改为”。认为鸟在A点时,影在A′点,当鸟到了相邻的B点,影也到了相邻的B′点,此时A′上的影已经消失,而在B′处另成了一个影,并非A′上的影移动到B′上来,这也是言之有理的。
机械运动只能在空间和时间中进行,运动体在单位时间内所经历的空间长度,就是速率。《墨经下》第65条之所述就包含着这方面的思想。《经说》云:“行,行者必先近而后远,远近,修也;先后,久也,民行修必以久也。”这里的文字是明明白白的,“修”指空间距离的长短,那意思是,物体运动在空间里必由近及远,其所经过的空间长度一定随时间而定,这里已有了路程随时间正变的朴素思想,也隐隐地包含着速率的观念了。
东汉时期的著作《尚书纬·考灵曜》中记载地球运动时说:“地恒动不止而人不知,譬如人在大舟中,闭牖(即窗户)而坐,舟行不觉也。”
这是对机械运动相对性的十分生动和浅显的比喻。哥白尼在叙述地球运动时也不谋而合地运用了十分类似的比喻。
|