实验数据的处理和分析（图象法）

　　图象可以反映物理量之间的变化关系，并便于找出其中的规律，确定对应量的函数关系；它可以将测量结果取平均值；可以由图象直接求出待测量。

　　描绘图象的要求是：

　　1．根据测量的要求选定坐标轴，一般以横轴为自变量，纵轴为因变量。坐标轴要标明所代表的物理量的名称及单位。

　　2．坐标轴的标度的选择应合适，使测量数据能在坐标轴上得到准确的反映。为避免图纸上出现大片空白，坐标原点可以是零，也可以不是零。坐标的标度值一般不必用有效数字表示，只要写明1，1．5，2，2．5，……即可，不必写成1．00，1．50，2．00，……。坐标轴的分度的估读数，应与测量值的估读数（即有效数字的末位）相对应。

　　3．根据测量所得数据，在图中标出坐标点。如同一坐标图上要描几条曲线，应分别用不同的符号，如“X”，“·”，“⊙”加以区别。

　　4．借助直尺或曲线板将图中的坐标点连成直线、折线或光滑曲线。注意并非所有的点都必须落在曲线上，但在线外的点应比较均匀地分布在线的两侧。个别偏差过大的点可以舍去或重新测量进行核对。

　　5．如要求计算直线的斜率，可以取直线上相隔较远的两点，不一定取由实验测出的用以描绘直线的数据点。

　　6．如果所研究的两个物理量不是成正比关系，可以变换坐标使其成为线性关系，从而得到一条直线。

　　例：利用上面的表格中的数据绘出电阻的阻值与温度的关系图线，如图1．7。

　　由图线可以看出，电阻的阻值与温度呈线性关系

R_t＝R₀＋k_tR_t

为任一温度t时的电阻值，R₀是纵轴上的截距，为0℃时的的电阻值。k为直线的斜率，它的物理意义是温度每变化1℃，电阻阻值的变化量。

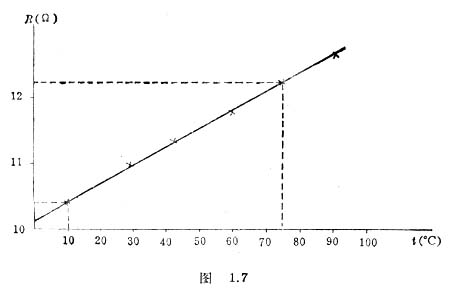
　　从图上可得R₀＝10．08欧。

　　由以上可以看出，运用图象不仅能直接看出两个量之间的变化关系，在一定的条件下延伸图象可以找到在测量范围之外的两物理量的对应值（外推法），也可以确定在测量范围之内的未进行测量的两物理量之间的对应值（内插法）。