研究气压随高度的变化关系

来研究气压随高度的变化关系，同时还可以学到一种应用图线求某点高度的方法。

　　方案一应用气态方程的实验

　　取一端封闭且粗细均匀的细玻璃管（约50—60厘米长），刻度尺，水银温度计（尽可能选准确度高的），注射针筒，水银气压计和少许水银备用。

　　用注射器把少量水银注入一端封闭的玻璃管，并借助一根干净的细钢丝使这段水银柱停留在离管口8—10厘米处。在实验室里把玻璃管水平放置（用气泡水准器校正水平），测出玻璃管中被水银密封的空气柱的长度L₀，如图（一）3．48－1所示，同时测出气温t₀和实验室里大气压强的值P₀。

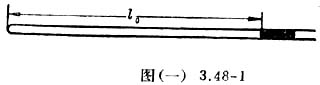
　　然后把玻璃管和温度计等带到高楼的底层（或山脚下），仍然水平放置玻璃管，测出密封气柱的长度L_A，以及当地的温度t_A，由理想气体的状态方程P₀L₀／T₀＝P_AL_A／T_A，可以求得A处的大气压强P_{A＝L0TAP0／LAT0。同样在第6层楼、第12}层楼、第18层楼等处（或者在山上几个已知相对高度的地点）分别重复上述实验测量步骤，算出相应的气压P_B、P_C……并根据楼层高度估算出B、C等层的高度。把你的测量数据记录在下列表中：

 

作P－H图象。

【思考题】

　　1．你作出的图线是否为线性的？误差的原因有哪些？

　　2．你能否根据实验图象求出实验室相对A点的高度？如果要知道你所途经的其他某处的高度，需要在那里做什么样的测量？

　　3．如果没有水银气压计和温度计，你能够应用玻意耳定律设计一个实验方案吗？但必须考虑到通常各测量点的温度是不一致的。

　　方案二应用查理定律的实验

　　如图（一）3．48－2所示，带有弯管的烧瓶，广口保温瓶，温度计和热水。

【方法与要求】

　　向保温瓶中注入热水。在烧瓶弯管的水平管中注入一段液体，并在管上液柱的一边作一个记号，测出保温瓶中热水的温度t₀。再把这个装置拿到某层楼A处，由于气压降低，液柱将向外移。在保温瓶中加少量冷水，并搅拌使温度分布均匀，直至液柱回到原来的记号位置，测出水温t_A。同样在其他层楼B、C处实验，测出相应的温度t_B、t_C。

　　由于上述过程为等容过程，根据查理定律P∝T，因此知道T与H的关系，也就可以知道p与H的关系。如果将保温瓶等移到不知其高度的地方，测出烧瓶内气体体积不变时的温度t_x，算出绝对温度T_x，根据T－H图线即可估计出高度。

选自：《高中物理课外实验》