间接测量误差

　　推算最终答案时，我们要将所得到的观测数据进行各种数学演算。因此，必须考虑如何从观测数据的误差计算出答案的误差。

　　如果从几个量相加或相减，其结果的绝对误为各量的误差之和。假设下面两个温度是在同一次实验中观测到的，要求确定温度的升高：

　　初温为11．0±0．5℃

　　终温为39．0±0．7℃欲求温度变化，我们从39．0减去11．0，得到28．0℃。其绝对误差为±1．2℃，它是将两个误差相加得到的。

　　这个结果是合理的，我们不妨说详细些。注意到两个观测量的实际含义是：

　　初温在10．5℃－11．5℃之间。

　　终温在38．3℃－39．7℃之间。考虑到极端情况，初温可能为10．5℃而终温可能为39．7℃，温升相应为29．2℃；另一种情况则可能是，温度从11．5℃上升到38．3℃，即温升仅为26．8℃（我们原来的表达式认为两种变比都是可能的）。这样，我们必须将答案记为（两个极值的平均值）±（它们差值的一半），即

，

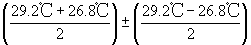　　也就是28．0℃±1．2℃。

　　如果几个量作乘、除运算，运算结果的实际误差用百分误差表示，那么结果的百分误差等于各量的百分误差之和。例如在前面的例子中，没获得相应温度变化的时间为150±3s，把前面已得到的数据除以相应的时间，即为温度的平均时间变化率。为此，我们作下面的计算：

　　时间的百分误差为±2％，温度变化即温升的百分误差为（1．2／28）×100％，约等于4．3％，因而温度的平均时间变化率的百分误差为±（2＋4．3）％，即为±6．3％，而温度的平均时间变化率则为（0．187±0．012）℃／S。