非线性图象

　　将结果直接画出来所得到的图象如果不是直线，仍然可能有个简单的方程式表示变量间的关系。并且，这样的关系式有可能变换成线性关系从而得到直线图解，这种变换步骤数学中称为“变量替换”。实际上，我们不是在改变实验中的物理量，“变量替换”纯属简化运算的数学手段。这点通过验证玻意耳定律的实验会更加清楚。定律的方程式为

PV＝k，

其中P是压强，V是体积，k是常量。P－V的图象不是直线，而是双曲线，如图4／6所示。但是，我们作出P－1／V的图象，就得到了关系式的图象，在式中x是1／V，这个图象是斜率为k的直线（图4／7）。数学上将x视为新的变量，但实验中V仍是自变量。变量替换可以使我们计算出k，而从p－V图象中却做不到。

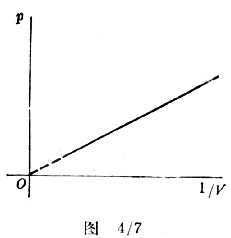
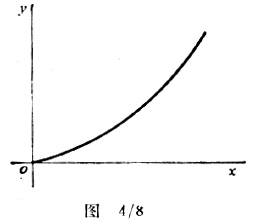
　　实际问题往往不这么简单，常常是我们并不知道变量间的关系式，而要去找到它。物理学中有许多常见的现象，其实验曲线不可能迅速地表达为一个确切的关系式（有时实验误差使之更难以表达）。这样，往往难以认定曲线所表达的关系是y＝x²还是y＝x³（如果实验曲线与两者的图象都有些相似的话）。这方面的问题可以简述为“如何设法把一个未知方程的曲线变换成一条直线，从而导出该方程”，当然，我们可以采用反复试验对照的方法，假如我们得到了图4／8所示的通过原点的一条曲线，不妨尝试作出y－x²的图象与之对照，如果失败，可再尝试作出y－x³的图象与之对照……直到满意为止。很明显，这样做既费时又不科学。这里有必要再次求助于教学。如果我们作出Logy－Logx的图象，假定实验曲线的关系式为y＝kx^m，其中k及m均为未知数，则Logy－Logx的图象就是一条直线，其斜率为x的幂指数m，其截距则为Logk。这是因为：将y＝kx^m两边取对数，得到

Logy＝Logk＋mLogx，

即

Logy＝mLogx＋Logk

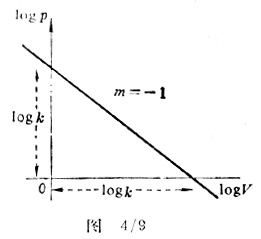
　　若令Y＝Logy，C＝Logk，X＝Logx，则上式就代表直线Y＝mx＋C，这就更容易得到上述论证。注意到它对于正、负幂指数及分数幂指数均适用，因而是很有效的方法。如对于玻意耳定律就可以这样作曲线。设想一位不知道这个定律的学生，从实验得到如图4／6所示的曲线，他作出LogP－LogV曲线是图4／9所示的直线，可以看出它的斜率是－1，从任一坐标轴上都可以找出截距Logk（因为两个截距是相等的），由此他得到P＝kV^－1，而且可以知道k的值。这样，通过作出两个图象，问题就得到了解决，这个解答可以由p－1／V图象验证。