第二节 运用公式法

教学重点和难点：

重点：平方差公式或完全平方公式。

难点：灵活运用平方差公式或完全平方公式分解因式。

教学建议:

1.     教材分析

(1)  知识结构:本小节首先说明什么叫做运用公式法,然后,依次介绍了平方差公式或完全平方公式,并结合公式讲授如何运用公式进行多项式的因式分解.

(2)  重点、难点分析

1)     弄清平方差公式的形式和特点，熟练地掌握公式。

平方差公式：

= .

这里 可以表示数、单项式、多项式.

①     左侧为两项;

②     两项都是平方项;

③     两项的符号相反.

2)       弄清完全平方公式的形式和特点,熟练地掌握公式.

完全平方公式:

这里 可以表示数、单项式、多项式.

公式的特点是:

①     左侧为三项:

②     首、末两项是平方项，并且首末两项的符号相同；

③     中间项是首末两项的底数的积的2倍。

3) 继续学会运用“把一个代数式看作一个字母”的换元思想，观察式子，提高处理式子变形的能力．

    　　运用公式分解因式的关键，是要通过“把一个代数式看作一个字母”的换元思想，把多项式向公式的形式化归，当多项式的结构特征符合公式的特征时，按照公式的另一边的结构，就可以直接写出分解的方法：

例如，分解二项式 时，关键的步骤是把 看作 ，把9看作 ，再把 看作a，把3看作b，于是就完成了式子 向公式左边 的化归：

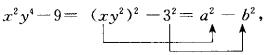
也就得到分解的方法：

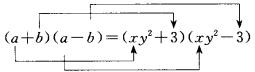
即

　　又如，分解 时，关键的步骤是把 看作 ，把 看作 ，从而中间“项”就可以看作 ；再把 看作a，把 看作b，于是就完成了式子 向公式左边 的化归：

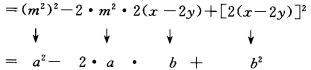
于是就可以依公式直接写出分解的结果

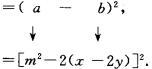
也就是有

 4) 掌握好运用公式团式分解，首先要学会幂的运算性质的逆方向的应用．

由于乘法公式中多处出现 （或 ）和 （或 ），所以被分解的多项式中，必须有可以化归为一个式子的平方成立方的项．这时，就要逆用幂的运算性质（m、n是自然数）：

，                 ①

．                      ②

例如，前例中，把 看作 的过程，依据的是：

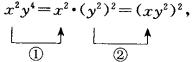
把 看作 的过程，依据的是

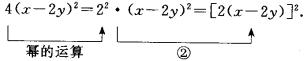
    只有弄清这些变形的细节，了解每步变形的依据，才是真正理解了分解变形的逻辑，掌握了分解的方法．

5) 怎样处理分数系数的多项式的因式分解？

    一般地说，多项式的因式分解是在系数是整数的多项式中进行的，但有时，对系数中含有分数（或小数）的多项式也可以进行这样的变形．这时，将有多种处理方法，分解结果也可能有不同的形式．

    例如，把下列多项式分解因式：

   （1）           （2）

解：（1）提出分数 ，使括号内的多项式是整数系数，再作分解，有

   （2）解法一：由于 ，提出分数 ，使括号内的多项式是整数系数的多项式，再作分解，有

解法二：直接运用公式得

可以看到，当多项式含有分数系数时，可以把一个适当分数提到括号外，使括号内是整数系数的多项式，然后作分解；如果可能，也可以直接作分解的变形，在第（1）小题中，事实上，有

这两种解法的结果是相同的．

    由分析可知，当把分数 提到括号里面时，只需把原多项式各项的系数分别乘以 （即 的倒数），就是括号内多项式相应各项的系数．

    一般地，为了使系数是分数的多项式的分解有唯一的结果，我们不妨规定，首先提一个适当的分数于括号外，使得括号内化为整系数的多项式，再作进一步的分解．

例如，把多项式 分解因式：

解：