 设为首页
设为首页
 加入收藏
加入收藏
教学建议
1、教材分析
(1)知识结构

(2)重点、难点、关键点分析
①重点:垂径定理及其推论是学习圆的工具性知识之一,它反映了圆的重要性质,是证明线段相等、角相等、垂直关系的重要依据,同时也为进行圆的计算和作图提供了方法和依据,所以这部分内容是本节的重点也是教材的重点.
②难点:垂径定理及推论的题设和结论较为复杂,很容易混淆,因此,它是本节的难点.
③关键点:教科书充分利用圆的对称性质来探讨圆的其他性质,如利用圆是轴对称图形(而且每一直径都是一个对称轴)直接推出“垂径定理”及推论,而又利用圆是一个中心对称圆形这一点,推出了弦,弦心距,弦之间的关系的一些定理及推论.因此,掌握圆的对称性质是学习圆的性质的关键之一,掌握了圆的对称性,就很容易推出圆的其他性质,利用圆的对称性,还可以使一些关于圆的命题的证明变得比较简单.
2、教法建议
本节需要三个课时.
(1)第一课时的主要内容是圆的对称性和垂径定理.在教学活动中,不管那个层次的学生,都通过学生动手实验、观察、理解圆的性质(轴对称、中心对称、旋转不变),并进一步组织学生实验、观察、发现新问题,探究和解决问题,完成对垂径定理的学习.
(2)第二课时的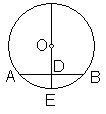 内容是垂径定理的推论.在教学活动中,对A层的学生老师组织自主学习,使学生把垂径定理的条件与结论解体并重新组合,学生通过小组交流,师生交流和对话中,概括出推论内容;对于B、C层的学生,老师引导学生观察、比较、分析、概括得到新知识.对不同层次的学生主要是组织形式上的差异.
内容是垂径定理的推论.在教学活动中,对A层的学生老师组织自主学习,使学生把垂径定理的条件与结论解体并重新组合,学生通过小组交流,师生交流和对话中,概括出推论内容;对于B、C层的学生,老师引导学生观察、比较、分析、概括得到新知识.对不同层次的学生主要是组织形式上的差异.
(3)第三课时的内容是垂径定理及其推论的应用.教师要利用实际问题、与新知识有关的计算和证明问题(如:如图在⊙O中,设⊙O半径为R,弦AB=a,弦心距OD=d,弓形的高DE=h,且OE⊥AB于D.已知:①R、d求a、h;②R、h求a、d;③R、a求d、h;④ d、h求R、a),为学生创造一个应用垂径定理及其推论的情境,让学生在分析问题、解决问题、归纳和反思,充分发挥学生学习的主动性与自觉性,提高学习的整体质量.