第五节 抛物线及其标准方程

教学建议

教材分析

1．  知识结构

2．重点难点分析

　　重点是抛物线的定义及标准方程；难点是标准方程及解直线与抛物线有关的综合问题．

　　（1）椭圆、双曲线、抛物线都是到定点 的距离和到定直线 的距离比为常数 的点的轨迹，这个定点是它们的焦点，定直线是它们的准线， 是它们的离心率．当 ， ， 时，这种轨迹分别表示椭圆、双曲线和抛物线．在直角坐标系下，它们的方程都是二次方程；这三种曲线都可以由平面截圆锥而得到．因而它们统称为二次曲线或圆锥曲线．

　　（2）对抛物线定义的理解，应注意定点不在定直线上，否则抛迹是一条直线．

　　（3）在推导抛物线方程的过程中，要注意领会如何建立坐标系．由抛物线定义可知，直线 是抛物线的对称轴，所以把 作为 轴可以使方程不出现 的一次项；因为线段 的中点适合条件，所以它在抛物线上，因而以 的中点作为原点，就可以使方程中不出现常数项．这样建立坐标系，得到的方程较为简单．

　　（4）由于建立坐标系的方法不同，抛物线的方程有四种不同形式： ， ， ， ．教科书上对方程与图形的关系，各种标准方程下的焦点坐标和准线方程，列表进行了对比，从而我们可以归纳出以下几个要点：

　　① 的几何意义：焦参数 是焦点到准线的距离，所以 恒为正数；

　　②方程有边一次项的变量与焦点所在坐标轴的名称相同，一次项系数的符号决定抛物线的开口方向；

　　③焦点的非零坐标（指 或 ）是一次项系数的 ．

　　④准线与坐标轴的交点与抛物线焦点关于原点对称．

　　（5）处理直线与抛物线的位置关系，类似于处理直线与椭圆、双曲线的关系．一般地，处理直线与圆锥曲线的位置关系，都是通过研究方程组解的个数，用判别式来进行判别．其中有两个比较容易忽略的地方：

　　①是否考虑了没有斜率的直线；

　　②对于双曲线是否考虑了与渐近线平行的直线，对于抛物线是否考虑了与对称轴平行的直线．反应到方程上，就是是否考虑了消去一个未知数后得到的方程二次项系数是否会为0．要把直线与圆锥曲线相切和相交区分开来．

　　（6）关于圆锥曲线弦长的计算．设斜率为 的直线交圆锥曲线于 ， ，则计算 的方法可以有以下几种：

　　①利用弦长公式

            或 计算；

　　②若 过圆锥曲线的焦点 ，可利用匾锥曲线的几何性质简化运算，即将 写成 ，再将 ， 转换成 ， 到相应准线距离的 倍．

　　以上两种方法一般都要结合韦达定理来进行．

教法建议

　　（1）椭圆的定义很简单但非常重要，教学时要注意和椭圆、双曲线的第二定义相联系，为深刻体会圆锥曲线的统一定义做好准备．

　　（2）在教学抛物线的标准方程时，应注意把位置特征（标准位置）和方程的特点（标准方程）统一起来，注意以下两点：

　　①   要让学生把握顶点、对称轴、开口方向与方程形式的对应关系：

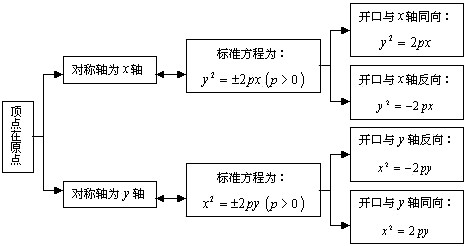
　　②已知抛物线的标准方程求其焦点坐标和准线方程时，可以根据二次项、一次项的分布画一个草图，进行初步的“定位”；再根据2p的数值来“定量”，即求出 的值．然后把两者结合起来即可．

　　（3）教学时要注意让学生区分抛物线和双曲线的一支，初学者很容易将抛物线与双曲线的一支混淆．二者区别在于：当抛物线上的点趋向于无穷远时，抛物线在这一点的斜率（曲线在某一点的斜率是指曲线在这一点的切线的斜率）接近于坐标轴所在直线的斜率，也就是抛物线接近于和坐标轴所在直线平行；而双曲线上的点趋向于无穷远时，它的斜率接近于它的渐近线的斜率．

返回页首