第四节 动量守恒定律的应用

动量守恒定律的应用的教学过程设计

　　本节是继动量守恒定律之后的习题课.主要巩固所学知识，学会在不同条件下，熟练灵活的运用动量守恒定律解释一些碰撞现象，并能利用动量守恒定律熟练的解决相关习题.

1、讨论动量守恒的基本条件

　　例1、在光滑水平面上有一个弹簧振子系统，如图所示，两振子的质量分别为m₁和m₂.讨论此系统在振动时动量是否守恒？

　　分析：由于水平面上无摩擦，故振动系统不受外力(竖直方向重力与支持力平衡)，所以此系统振动时动量守恒，即向左的动量与向右的动量大小相等.

　　例2、接上题，若水平地面不光滑，两振子的动摩擦因数μ相同，讨论m₁＝m₂和m₁≠m₂两种情况下振动系统的动量是否守恒.

　　分析：m₁和m₂所受摩擦力分别为f₁＝μm₁g和f₂＝μm₂g.由于振动时两振子的运动方向总是相反的，所以f₁和f₂的方向总是相反的.

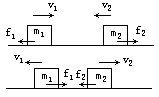
　　对m₁和m₂振动系统来说合外力∑F外＝f₁+f₂，但注意是矢量合.实际运算时为

　　∑F外＝μm₁g-μm₂g

　　显然，若m₁＝m₂，则∑F外＝0，则动量守恒；

　　若m₁≠m₂，则∑F外≠0，则动量不守恒.

向学生提出问题：

　　(1)m₁＝m₂时动量守恒，那么动量是多少？

　　(2)m₁≠m₂时动量不守恒，那么振动情况可能是怎样的？

与学生共同分析：

　　(1) m₁＝m₂时动量守恒，系统的总动量为零.开始时(释放振子时)p＝0，此后振动时，当p₁和p₂均不为零时，它们的大小是相等的，但方向是相反的，所以总动量仍为零.

数学表达式可写成：

　　m₁v₁＝m₂v₂

　　(2) m₁≠m₂时∑F外＝μ(m₁-m₂)g.其方向取决于m₁和m₂的大小以及运动方向.比如m₁＞m₂，一开始m₁向右(m₂向左)运动，结果系统所受合外力∑F方向向左(f₁向左，f₂向右，而且f₁＞f₂).结果是在前半个周期里整个系统一边振动一边向左移动.

进一步提出问题：（如果还没有学过机械能守恒此部分可省略）

　　在m₁＝m2的情况下，振动系统的动量守恒，其机械能是否守恒？

　　分析：振动是动能和弹性势能间的能量转化.但由于有摩擦存在，在动能和弹性势能往复转化的过程中势必有一部分能量变为热损耗，直至把全部原有的机械能都转化为热，振动停止.所以虽然动量守恒(p＝0)，但机械能不守恒.(从振动到不振动)

　　2、学习设置正方向，变一维矢量运算为代数运算

　　例3、抛出的手雷在最高点时水平速度为10m/s，这时突然炸成两块，其中大块质量300g仍按原方向飞行，其速度测得为50m/s，另一小块质量为200g，求它的速度的大小和方向.

　　分析：手雷在空中爆炸时所受合外力应是它受到的重力G＝(m₁+m₂)g，可见系统的动量并不守恒.但在水平方向上可以认为系统不受外力，所以在水平方向上动量是守恒的.

　　强调：正是由于动量是矢量，所以动量守恒定律可在某个方向上应用.

　　那么手雷在以10m/s飞行时空气阻力(水平方向)是不是应该考虑呢？

　　(上述问题学生可能会提出，若学生没有提出，教师应向学生提出.)

　　一般说当v＝10m/s时空气阻力是应考虑，但爆炸力(内力)比这一阻力大的多，所以这一瞬间空气阻力可以不计.即当内力远大于外力时，外力可以不计，系统的动量近似守恒.

板书：F内>>F外时p′≈p.

解题过程：

　　设手雷原飞行方向为正方向，则v₀＝10m/s，m₁的速度v₁＝50m/s，m2的速度方向不清，暂设为正方向.

板书：

　　设原飞行方向为正方向，则v₀＝10m/s，v₁＝50m/s；m₁＝0.3kg，m₂＝0.2kg.

系统动量守恒：

　　(m₁+m₂)v0＝m₁v₁+m₂v₂

　　

　　此结果表明，质量为200克的部分以50m/s的速度向反方向运动，其中负号表示与所设正方向相反.

　　例4、机关枪重8kg，射出的子弹质量为20克，若子弹的出口速度是1 000m/s，则机枪的后退速度是多少？

　　分析：在水平方向火药的爆炸力远大于此瞬间机枪受的外力(枪手的依托力)，故可认为在水平方向动量守恒.即子弹向前的动量等于机枪向后的动量，总动量维持“零”值不变.

板书：

　　设子弹速度v，质量m；机枪后退速度V，质量M.则由动量守恒有

　　MV＝mv



　　小结：上述两例都属于“反冲”和“爆炸”一类的问题，其特点是F内>>F外，系统近似动量守恒

　　例5、讨论质量为m_A的球以速度v0去碰撞静止的质量为m_B的球后，两球的速度各是多少？设碰撞过程中没有能量损失，水平面光滑.

　　设A球的初速度v₀的方向为正方向.

　　由动量守恒和能量守恒可列出下述方程：

　　

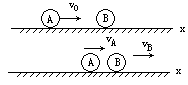
　　m_Av0＝m_Av_A+m_Bv_B          ①



解方程①和②可以得到



引导学生讨论：

　　(1)由v_B表达式可知v_B恒大于零，即B球肯定是向前运动的，这与生活中观察到的各种现象是吻合的.

　　(2)由v_A表达式可知当m_A＞m_B时，v_A＞0，即碰后A球依然向前滚动，不过速度已比原来小了 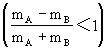。当 时， ，即碰后A球反弹，且一般情况下速度也小于v₀了.当m_A＝m_B时，v_A＝0，v_B＝v₀，这就是刚才看到的实验，即A、B两球互换动量的情形.

　　(3)讨论极端情形：若m_B→∞时，v_A＝-v0，即原速反弹；而v_B→0，即几乎不动.这就好像是生活中的小皮球撞墙的情形.（在热学部分中气体分子与器壁碰撞的模型就属于这种情形）.

　　(4)由于v_A总是小于v₀的，所以通过碰撞可以使一个物体减速（在核反应堆中利用中子与碳原子(石墨或重水)的碰撞将快中子变为慢中子）.

3、动量守恒定律是对同一个惯性参照系成立的.

　　例6  质量为M的平板车静止在水平路面上，车与路面间的摩擦不计.质量为m的人从车的左端走到右端，已知车长为L，求在此期间车行的距离？

　　分析：由动量守恒定律可知人向右的动量应等于车向左的动量，即：mv＝MV

　　用位移与时间的比表示速度应有（x为车行的距离）：



　　解得

讨论：这里容易发生的错误是 ，结果得到 。

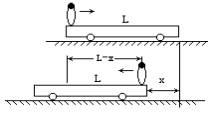
　　动量守恒定律中的各个速度必须是对同一个惯性参照系而言的速度，而将V写成L/t是在小车参照系中的速度，不是地面参照系的速度，以致发生上述错误.

4、总结：使用动量守恒定律要注意：

　　第一、所研究的系统如果满足F外<<F内时，可以近似地认为动量守恒.

　　第二、所研究的系统是否动量守恒或在某一方向上动量守恒.

　　第三、列动量守恒式时，应注意式中所有的速度都是对同一个惯性参照系而言的.

　　第四、为了不混淆速度方向，一般应先确定一个正方向，以此来确定各个速度的方向，然后以代数计算替换一维矢量计算.