第四节 不等式的解法举例

分式不等式的解法

教学目标

　　1．掌握分式不等式向整式不等式的转化；
　　2．进一步熟悉并掌握数轴标根法；
　　3．掌握分式不等式基本解法.

教学重点难点

　　重点是分式不等式解法
　　难点是分式不等式向整式不等式的转化

教学方法

　　启发式和引导式

教具准备

　　三角板、幻灯片

教学过程

1．复习回顾：

　　前面，我们学习了含有绝对值的不等式的基本解法，还了解了数轴标根法的解题思路，本节课，我们将继续研究分式不等式的解法.

2．讲授新课：

例3  解不等式 ＜0.

　　分析：这是一个分式不等式，其左边是两个关于x的二次三项式的商，根据商的符号法则，它可以化成两个不等式组：

　　因此，原不等式的解集就是上面两个不等式组的解集的并集，此种解法从课本可以看到.

　　另解：根据积的符号法则，可以将原不等式等价变形为（x²－3x＋2）(x²－2x－3)＜0

　　即（x＋1）(x－1)(x－2)(x－3)＜0

　　令（x＋1）(x－1)(x－2)(x－3)=0

　　可得零点x=－1或1，或2或3，将数轴分成五部分（如图）.

　　由数轴标根法可得所求不等式解集为：

　　{x|－1＜x＜1或2＜x＜3}

　　说明：（1）让学生注意数轴标根法适用条件；

　　（2）让学生思考 ≤0的等价变形.

例4  解不等式 ＞1

　　分析：首先转化成右端为0的分式不等式，然后再等价变形为整式不等式求解.

　　解：原不等式等价变形为：

 －1＞0

　　通分整理得： ＞0

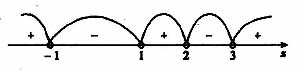　　等价变形为：（x²－2x＋3）(x²－3x＋2)＞0

　　即：（x＋1）(x－1)(x－2)(x－3)＞0

　　由数轴标根法可得所求不等式解集为：

　　　　{x|x＜－1或1＜x＜2或x＞3}

　　说明：此题要求学生掌握较为一般的分式不等式的转化与求解.

3．课堂练习：

　　课本P₁₉练习1.

　　补充：（1） ≥0；

　　　　　（2）x(x－3)(x＋1)(x－2)≤0.

课堂小结

　　通过本节学习，要求大家在进一步掌握数轴标根法的基础上，掌握分式不等式的基本解法，即转化为整式不等式求解.

课后作业

　　习题6.4  3,4.

板书设计

●教学后记

返回顶部