 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例(一)
教学目标
掌握抛物线的定义,会推导抛物线的标准方程,能根据已知条件熟练地求出抛物线的标准方程.
教学过程
情境设置
我们知道,与一个定点的距离和一条定直线的距离的比是常数 ![]() 的点的轨迹,当
的点的轨迹,当 ![]() 时是椭圆,当
时是椭圆,当 ![]() 时是双曲线,那么当
时是双曲线,那么当 ![]() 时是什么曲线呢?这就是今天我们要学习的第三种圆锥曲线一一抛物线,以及它的定义和标准方程.板书课题“抛物线及其标准方程”.
时是什么曲线呢?这就是今天我们要学习的第三种圆锥曲线一一抛物线,以及它的定义和标准方程.板书课题“抛物线及其标准方程”.
请大家思考两个问题:
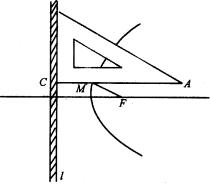
问题1.同学们对抛物线已有了哪些认识?
在物理学中,抛物线被认为是斜抛物体的运动轨道;在数学中,抛物线是二次函数的图像.
问题2.在二次函数中研究的抛物线,它的对称轴平行于 ![]() 轴,开口向上或开口向下两种情形.
轴,开口向上或开口向下两种情形.
如果抛物线的对称轴不平行于 ![]() 轴,那么就不能作为二次函数的图像来研究了.今天我们突破函数研究中的限制,从更一般的意义上来研究抛物线.
轴,那么就不能作为二次函数的图像来研究了.今天我们突破函数研究中的限制,从更一般的意义上来研究抛物线.
如图,把一根直尺固定在图板内直线 ![]() 的位置,一块三角板的一条直角边紧靠直尺的边缘.再把一条钢绳的一端固定于三角板的另一条直角边上的点
的位置,一块三角板的一条直角边紧靠直尺的边缘.再把一条钢绳的一端固定于三角板的另一条直角边上的点 ![]() ,截取绳子的长等于
,截取绳子的长等于 ![]() 到直线
到直线 ![]() 的距离
的距离 ![]() ,并且把绳子的另一端固定在图板上的一点
,并且把绳子的另一端固定在图板上的一点 ![]() ;用一支铅笔扣着绳子,紧靠着三角板的这条直角边把绳子绷紧,然后使三角板紧靠着直尺上下滑动,这样铅笔描出一条曲线,这条曲线就叫做抛物线.
;用一支铅笔扣着绳子,紧靠着三角板的这条直角边把绳子绷紧,然后使三角板紧靠着直尺上下滑动,这样铅笔描出一条曲线,这条曲线就叫做抛物线.
【探索研究】
1.抛物线的定义
反复演示后可以看出,这条曲线上任意一点 ![]() 到
到 ![]() 的距离与它到直线
的距离与它到直线 ![]() 的距离相等,请一名学生来归纳抛物线的定义:
的距离相等,请一名学生来归纳抛物线的定义:
平面内与一个定点 ![]() 和一条定直线
和一条定直线 ![]() 的距离相等的点的轨迹叫做抛物线.点
的距离相等的点的轨迹叫做抛物线.点 ![]() 叫做抛物线的焦点,定直线
叫做抛物线的焦点,定直线 ![]() 叫做抛物线的准线.
叫做抛物线的准线.
2.抛物线的标准方程
设定点 ![]() 到定直线
到定直线 ![]() 的距离为
的距离为 ![]() .
.
下面我们来求抛物线的方程,先让学生根据自己的思考建立坐标系,求出抛物线的方程,教师巡视,从学生的求法中归纳出以下几种方案:
方案一:(请一名学生完成)
 以
以 ![]() 为
为 ![]() 轴,过点
轴,过点 ![]() 垂直于
垂直于 ![]() 的直线为
的直线为 ![]() 轴建立直角坐标系(如图8-28),则定点
轴建立直角坐标系(如图8-28),则定点 ![]() .
.
设动点 ![]() ,由抛物线定义得:
,由抛物线定义得: ![]()
化简后得: ![]()
方案二:(请一名学生完成)
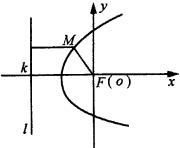 以定点
以定点 ![]() 为原点,过点
为原点,过点 ![]() 垂直于
垂直于 ![]() 的直线为
的直线为 ![]() 轴建立直角坐标系(如图),则
轴建立直角坐标系(如图),则 ![]() ,
, ![]() 的方程为
的方程为 ![]() . 设动点
. 设动点 ![]() ,由抛物线定义得:
,由抛物线定义得: ![]()
化简后得: ![]()
![]()
方案三:(请一名学生完成)
 取过焦点
取过焦点 ![]() 且垂直于准线
且垂直于准线 ![]() 的直线为
的直线为 ![]() 轴,
轴, ![]() 轴与
轴与 ![]() 交于
交于 ![]() ,以线段
,以线段 ![]() 的垂直平分线为
的垂直平分线为 ![]() 轴建立直角坐标系(如图 ),则
轴建立直角坐标系(如图 ),则 ![]() .
.
![]() 的方程为
的方程为 ![]() .
.
设动点 ![]() ,由抛物线定义得
,由抛物线定义得

化简后得: ![]()
![]()
通过比较可以看出,方案3得出的方程不仅具有较简的形式,而且方程中一次项的系数是焦点到准线距离的2倍。
这个方程叫做抛物线的标准方程,它表示抛物线的焦点在 ![]() 轴的正半轴上,坐标是
轴的正半轴上,坐标是 ![]() ,准线方程是
,准线方程是 ![]() .
.
一条抛物线,由于它在坐标系的位置不同,方程也不同,有四种不同的情况,如下表:
|
图形 |
标准方程 |
焦点坐标 |
准线方程 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
将上表画在小黑板上(或投影胶片上),并讲清为什么会出现四种不同的情况,分析方程的特点。
【例题分析】
例题(1)已知抛物线的标准方程 ![]() ,求它的焦点坐标和准线方程;
,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是 ![]() ,求它的标准方程。
,求它的标准方程。
解:(1)因为 ![]() ,
, ![]() ,所以焦点坐标是
,所以焦点坐标是 ![]() ,准线方程是
,准线方程是 ![]() .
.
(2)因为焦点在 ![]() 轴的负半轴上,并且
轴的负半轴上,并且 ![]() ,
, ![]() ,所以抛物线的标准方程是
,所以抛物线的标准方程是 ![]() .
.
(三)随堂练习
1.根据下列条件写出抛物线的标准方程
①焦点是 ![]() ;②准线方程是
;②准线方程是 ![]() ;③焦点到准线的距离是2
;③焦点到准线的距离是2
2.求下列抛物线的焦点坐标和准线方程
① ![]() ②
② ![]() ③
③ ![]() ④
④ ![]()
3.①抛物线 ![]() 上一点
上一点 ![]() 到焦点的距离是
到焦点的距离是 ![]() ,则点
,则点 ![]() 到准线的距离是__________,点
到准线的距离是__________,点 ![]() 的横坐标是__________,
的横坐标是__________,
②抛物线 ![]() 上与焦点的距离等于9的点的坐标是_________.
上与焦点的距离等于9的点的坐标是_________.
答案:1. ① ![]() ②
② ![]() ③
③ ![]()
2.① ![]() ,
, ![]() ②
② ![]() ,
, ![]() .
.
③ ![]() ,
, ![]() ④
④ ![]() ,
, ![]()
3.① ![]() ②
② ![]() ,
, ![]()
(四)总结提炼
抛物线的标准方程有四种形式,(见上表), ![]() 的意义是表示焦点到准线的距离,因为焦点不在准线上,所以
的意义是表示焦点到准线的距离,因为焦点不在准线上,所以 ![]() ,当定点
,当定点 ![]() 在定直线
在定直线 ![]() 上时,到
上时,到 ![]() 的距离与到
的距离与到 ![]() 的距离相等的点的轨迹是过
的距离相等的点的轨迹是过 ![]() 与
与 ![]() 垂直的直线,标准方程中
垂直的直线,标准方程中 ![]() 前面的正负号决定了抛物线的开口方向。
前面的正负号决定了抛物线的开口方向。
(五)布置作业
1.准线方程为 ![]() 的抛物线的标准方程是( )
的抛物线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.抛物线 ![]() 的焦点坐标是( )
的焦点坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3.经过 ![]() 的抛物线的标准方程为_____________.
的抛物线的标准方程为_____________.
4.焦点在直线 ![]() 上的抛物线标准方程为_____________.
上的抛物线标准方程为_____________.
5.已知两条抛物线的焦点分别是
![]() 、
、 ![]() ,求它们的标准方程。
,求它们的标准方程。
6.动圆 ![]() 过
过 ![]() 且与直线
且与直线 ![]() 相切,求动圆圆心
相切,求动圆圆心 ![]() 的轨迹方程。
的轨迹方程。
答案:1.B 2.C 3. ![]() 或
或 ![]() 4.
4. ![]() 或
或 ![]() 5.
5. ![]() ,
, ![]() 6.
6. ![]()
(六)板书设计
|
8.5 抛物线及其标准方程(一) |
||
|
一、抛物线的定义 二、抛物线标准方程 列表 |
三、抛物线标准方程推导 |
四、例题分析 五、练习 六、小结 |
教学设计示例(二)
教学目标
能够熟练利用抛物线的定义解决问题,会求抛物线的焦点弦长.
教学过程
【复习引入】
由一名学生回答,教师板书.
问题:抛物线的定义是什么?
答:平均数面内与一个定点 ![]() 和一条定直线
和一条定直线 ![]() 的距离相等的点的轨迹叫做抛物线。
的距离相等的点的轨迹叫做抛物线。
抛物线的定义不仅反映了抛物线的本质,也为我们解决有关抛物线的问题提供了简捷的方法.
【探索研究】
例1 点 ![]() 与点到
与点到 ![]() 的距离比它到直线
的距离比它到直线 ![]() 的距离小1,求点
的距离小1,求点 ![]() 的轨迹方程.
的轨迹方程.
解:如图,设点 ![]() 的坐标为
的坐标为 ![]()
由已知条件,“点 ![]() 与点
与点 ![]() 的距离比它到直线
的距离比它到直线 ![]() ”
”
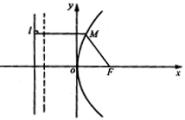 由已知条件,“点M与点F的距离比它到直线
由已知条件,“点M与点F的距离比它到直线
![]() 的距离小1”,就是“点M与点F的距离等于它到直线
的距离小1”,就是“点M与点F的距离等于它到直线
![]() 的距离”。根据抛物线的定义,点M的轨迹是以F(4,0)为焦点的抛物线。
的距离”。根据抛物线的定义,点M的轨迹是以F(4,0)为焦点的抛物线。
![]()
因为焦点在x轴的正半轴,所以点M的轨迹方程为 ![]() 。
。
点评:若将条件化为 ![]() ,其中
,其中 ![]() 用两点间距离公式表示,再化简得方程,但这种解决的化简过程比较繁琐。
用两点间距离公式表示,再化简得方程,但这种解决的化简过程比较繁琐。
例2 已知抛物线的顶点在原点,对称轴为
![]() 轴,抛物线上的点
轴,抛物线上的点 ![]()
![]() 到焦点的距离等于5,求抛物线的方程和
到焦点的距离等于5,求抛物线的方程和 ![]() 的值。
的值。
由一名学生演板,其他学生练习,然后教师订正,归纳两种方法加以比较,说明运用定义的方法简捷。
解法一:设抛物线方程为 ![]() ,则焦点
,则焦点 ![]() ,
,
由题设可得: 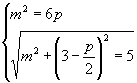
解得 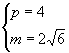 或
或 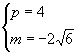
故抛物线方程为 ![]() 的值为
的值为 ![]()
解法二 设抛物线方程为
![]() ,则焦点
,则焦点 ![]() ,准线方程为
,准线方程为 ![]() .
.
根据抛物线定义, ![]() 到焦点的距离等于5,也就是
到焦点的距离等于5,也就是 ![]() 到准线的距离等于5,
到准线的距离等于5,
则 ![]()
![]()
![]()
因此抛物线方程为 ![]() .
.
又点 ![]() 在抛物线上,于是
在抛物线上,于是 ![]()
![]() .
.
点评:解法二利用抛物线的定义把到焦点的距离转化到准线的距离,既快捷又方便,要善于转化。
例3 斜率为1的直线经过抛物线 ![]() 的焦点,与抛物线相交于两点
的焦点,与抛物线相交于两点 ![]() 、
、 ![]() ,求线段
,求线段 ![]() 的长。
的长。
由一名学生演板,再由另一名学生补充其他解法,教师订正并归纳以下三种解法.
 如图,由抛物线的标准方程可知,焦点
如图,由抛物线的标准方程可知,焦点 ![]() ,准线方程
,准线方程 ![]() .
.
由题设,直线 ![]() 的方程为:
的方程为: ![]() .
.
代入抛物线方程 ![]() ,整理得:
,整理得: ![]() .
.
解法一:解上述方程得: ![]() ,
, ![]()
分别代入直线方程得: ![]()
![]()
即 ![]() 坐标分别为
坐标分别为 ![]() 、
、 ![]() .
.
![]()
![]()
解法二:设 ![]() ,
, ![]() ,则:
,则: ![]()
![]()
![]()
![]()
![]()
解法三:设 ![]() 、
、 ![]() . 由抛物线定义可知,
. 由抛物线定义可知, ![]() 等于点
等于点 ![]() 到准线
到准线 ![]() 的距离
的距离 ![]() .
.
即 ![]()
同理 ![]()
![]()
![]()
点拨:1.解法一利用传统的基本方法求出 ![]() 两点坐标,再利用两点间距离公式求出
两点坐标,再利用两点间距离公式求出 ![]() 的长。解法二没有直线求出
的长。解法二没有直线求出 ![]() 坐标。而是利用韦达定理找到
坐标。而是利用韦达定理找到 ![]() 与
与 ![]() 的关系,利用直线截二次曲线的弦长公式
的关系,利用直线截二次曲线的弦长公式 ![]() 求得,这是典型的设而不求思想方法比解法一先进,解法三充分利用抛物线的定义,把过焦点的这一特殊的弦分成两个半径的和,转化为准线的距离,这是思维质的飞跃。
求得,这是典型的设而不求思想方法比解法一先进,解法三充分利用抛物线的定义,把过焦点的这一特殊的弦分成两个半径的和,转化为准线的距离,这是思维质的飞跃。
2.抛物线 ![]() 上一点
上一点 ![]() 到焦点
到焦点 ![]() 的距离
的距离 ![]() 这就是抛物线的焦半径公式。焦点弦长
这就是抛物线的焦半径公式。焦点弦长 ![]()
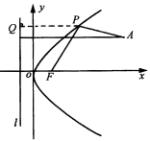
例4 在抛物线 ![]() 上求一点
上求一点 ![]() ,使
,使 ![]() 到焦点
到焦点 ![]() 与到点
与到点 ![]() 的距离之各最小。
的距离之各最小。
 由学生练习后,教师讲解。
由学生练习后,教师讲解。
解:如图,设抛物线上的点 ![]() 到准线的距离为
到准线的距离为 ![]() .
.
由抛物线定义可知: ![]()
显然当 ![]() 三点共线时,
三点共线时, ![]() 最小
最小
![]() ,可设
,可设 ![]() 代入
代入 ![]() 得
得 ![]() . 故点
. 故点 ![]() 的坐标为
的坐标为 ![]() .
.
(三)随堂练习
1.若抛物线 ![]() 上一点
上一点 ![]() 与焦点
与焦点 ![]() 的距离
的距离 ![]() ,则点
,则点 ![]() 的坐标为__________.
的坐标为__________.
2.已知抛物线方程为标准方程,焦点在 ![]() 轴上,抛物线上一点
轴上,抛物线上一点 ![]() 到焦点
到焦点 ![]() 的距离为5,则抛物线方程为__________,
的距离为5,则抛物线方程为__________, ![]() 的值等于_____________.
的值等于_____________.
3.过抛物线 ![]() 的焦点作直线交抛物线于
的焦点作直线交抛物线于 ![]() ,
, ![]() 两点,如果
两点,如果 ![]() ,则
,则 ![]() 的值为_______.
的值为_______.
答案:1. ![]() 2.
2. ![]() 3.8
3.8
(四)总结提炼
1.求抛物线的标准方程需判断焦点所在的坐标轴和确定 ![]() 的值,过焦点的直线与抛物线的交点问题有时用焦半径公式较简单。
的值,过焦点的直线与抛物线的交点问题有时用焦半径公式较简单。
2.焦点弦的几条性质:设直线过焦点 ![]() 与抛物线
与抛物线 ![]() 相交于
相交于 ![]() ,
, ![]() 两点,则:①
两点,则:① ![]() ;
②
;
② ![]() ③通径长为
③通径长为 ![]() ④焦点弦长
④焦点弦长 ![]() .
.
(五)布置作业
1.动点 ![]() 到点
到点 ![]() 的距离比到直线
的距离比到直线 ![]() 的距离小2,则动点
的距离小2,则动点 ![]() 的轨迹方程为( )
的轨迹方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2.直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 两点,且
两点,且 ![]() 的中心横坐标为2,则
的中心横坐标为2,则 ![]() 的值是( )
的值是( )
A. ![]() B.2
C.
B.2
C. ![]() 或2 D.以上都不对
或2 D.以上都不对
3.已知抛物线 ![]() 的焦点为
的焦点为 ![]() ,定点
,定点 ![]() ,在此抛物线上求一点
,在此抛物线上求一点 ![]() ,使
,使 ![]() 最小,则
最小,则 ![]() 点坐标为( )
点坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4.抛物线 ![]() 上纵坐标为2的点的焦半径等于4,则焦点到准线的距离是________.
上纵坐标为2的点的焦半径等于4,则焦点到准线的距离是________.
5.过抛物线 ![]() 的焦点的一条直线和此抛物线相交;两个交点的纵坐标为
的焦点的一条直线和此抛物线相交;两个交点的纵坐标为 ![]() ,求证:
,求证: ![]()
6.求证:以抛物线的焦点弦为直径的圆必与抛物线准线相切。
答案:
1.D 2.B 3.C 4.4
5.焦点 ![]() ,设过焦点
,设过焦点 ![]() 的直线方程为
的直线方程为 ![]()
 由
由  得
得 ![]()
由韦达定理得 ![]()
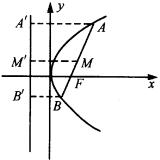
6.如图,作 ![]() 于
于 ![]() ,
, ![]()
![]() 于
于 ![]() ,
, ![]() 为
为 ![]() 的中心,作
的中心,作 ![]() ,则由抛物线定义可知
,则由抛物线定义可知
![]() ,
, ![]() 。在直角梯形
。在直角梯形 ![]() 中.
中.
![]()
![]()
即 ![]() 等于以
等于以 ![]() 为直径的圆的半径。
为直径的圆的半径。
故以 ![]() 为直径的圆心与抛物线的准线相切。
为直径的圆心与抛物线的准线相切。
(六)板书设计
|
8.5 抛物线及其标准方程(二) |
||
|
一、抛物线的定义 二、抛物线焦半径 焦点弦公式 |
例1 例2 |
例3 例4 练习 小结 |