 设为首页
设为首页
 加入收藏
加入收藏
例1——由动能定理解决电场中粒子的运动问题
图所示带电导体,已知其表面的电场强度 ![]() N/C,
N/C, ![]() N/C,点电荷q在电场力的作用下第一次由A点由静止释放到无限远处;第二次由B点由静止释放到无限远处。二次初始的加速度大小之比
N/C,点电荷q在电场力的作用下第一次由A点由静止释放到无限远处;第二次由B点由静止释放到无限远处。二次初始的加速度大小之比 ![]() ;二次的末速度大小之比
;二次的末速度大小之比 ![]() 。
。

解析:同一点电荷在A、B两点所受的电场力的大小与这两点的电场强度大小成正比。由牛顿第二定律可得 ![]() 。由于带电导体也是一个等势体,所以A、B两点的电势相等,它们与无限远处的电势差是相等的,电场力做功
。由于带电导体也是一个等势体,所以A、B两点的电势相等,它们与无限远处的电势差是相等的,电场力做功
![]() ,说明了这两次电场力做功是相等的电荷均由静止释放,由动能定理可知两次的末速度大小是相等的,即
,说明了这两次电场力做功是相等的电荷均由静止释放,由动能定理可知两次的末速度大小是相等的,即 ![]() 。
。
例2——关于电荷在交变电场中的运动情况分析
如图所示,A、B是一对平行的金属板,在两板间加上一周期为T的交变电压 ![]() 。A板的电势
。A板的电势 ![]() ,B板的电势
,B板的电势 ![]() 随时间的变化规律为:在0到
随时间的变化规律为:在0到 ![]() 时间内,
时间内, ![]() (正的常数);在
(正的常数);在 ![]() 到T的时间内,
到T的时间内, ![]() ;在T到
;在T到 ![]() 的时间内
的时间内 ![]() ;在
;在 ![]() 到2T的时间内,
到2T的时间内, ![]() ;…….现有一个电子从A板上的小孔进入两板间的电场区内.设电子的初速度和重力对它的影响均可忽略( )
;…….现有一个电子从A板上的小孔进入两板间的电场区内.设电子的初速度和重力对它的影响均可忽略( )
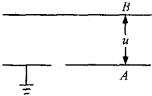
A、若电子是在 ![]() 时刻进入的,它将一直向B板运动
时刻进入的,它将一直向B板运动
B、若电子是在 ![]() 时刻进入的,它可能时而向B板运动,时而向A板运动,最后打在B板上
时刻进入的,它可能时而向B板运动,时而向A板运动,最后打在B板上
C、若电子是在 ![]() 时刻进入的,它可能时而向B板运动,时而向A板运动,最后打在B板上
时刻进入的,它可能时而向B板运动,时而向A板运动,最后打在B板上
D、若电子是在 ![]() 时刻进入的,它可能时而向B板、时而向A板运动
时刻进入的,它可能时而向B板、时而向A板运动
解析:依题意,A、B板间电场在 ![]() ,…,时间内场强方向为竖直向下;在
,…,时间内场强方向为竖直向下;在 ![]() ,…,时间内场强方向竖直向上.
,…,时间内场强方向竖直向上.
若电子在 ![]() 时刻进入板间,则在
时刻进入板间,则在 ![]() 时间内,将向B板加速运动,到
时间内,将向B板加速运动,到 ![]() 时刻,电子已获得一定的竖直向上的速度v,在
时刻,电子已获得一定的竖直向上的速度v,在 ![]() 时间内(电子也可能在此前或此间到达B板),电子受到的电场力反向,加速度方向与速度v方向相反,作匀减速运动.根据运动的对称性,到T时刻,粒子速度减为零,此后重复上述运动,直到到达B板时止.此过程可借助电子的
时间内(电子也可能在此前或此间到达B板),电子受到的电场力反向,加速度方向与速度v方向相反,作匀减速运动.根据运动的对称性,到T时刻,粒子速度减为零,此后重复上述运动,直到到达B板时止.此过程可借助电子的 ![]() 图像直观表示如图所示.故A对.
图像直观表示如图所示.故A对.

若电子在 ![]() 时刻进入,则电子在
时刻进入,则电子在 ![]() 时间内向B板加速运动,在
时间内向B板加速运动,在 ![]() 时间内向B板减速运动,到
时间内向B板减速运动,到 ![]() 时刻速度为零;在
时刻速度为零;在 ![]() 时间内反向向A板加速运动,在
时间内反向向A板加速运动,在 ![]() 时间内向A板减速运动,在
时间内向A板减速运动,在 ![]() 时刻,速度为零;在
时刻,速度为零;在 ![]() 时间内又向B板运动.如图所示.从图中还可判断,最终电子将到达B板。故B正确.
时间内又向B板运动.如图所示.从图中还可判断,最终电子将到达B板。故B正确.
类似分析可以判断C、D错误.本题正确选项为A、B。
例3——关于带电粒子在匀强电场中的加速偏转
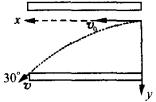
长为l的平行金属板,板门形成匀强电场,一个带电为+q、质量为m的带电粒子,以初速
![]() 紧贴上板垂直于电场线方向射入该电场,刚好从下板边缘射出,末速度恰与下板成30°,如图所示.求:
紧贴上板垂直于电场线方向射入该电场,刚好从下板边缘射出,末速度恰与下板成30°,如图所示.求:
(1)粒子求速度的大小;
(2)匀强电场的场强;
(3)两板间的距离d.
解法一、由牛顿定律和运动学公式求解
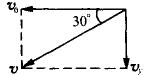
由速度矢量图(如图)得粒子末速度
![]()
粒子在电场中运动时间 ![]() ,粒子射出电场时活场强方向的分速度
,粒子射出电场时活场强方向的分速度 ![]()
由![]() 有
有 ![]() ,则场强
,则场强 ![]()
两板间距离 ![]()
解法二、由动量定理和动能定理求解.
![]()
由动量定理有 ![]()
由动能定理有 ![]()