 设为首页
设为首页
 加入收藏
加入收藏
典型例题
例1 下列各图中,表示数轴的是( )
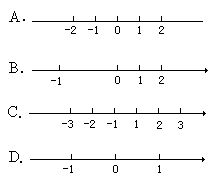
分析 画数轴时,数轴的三要素——原点、正方向、单位长度是缺一不可的,所以应当用这三要素检查每个图形,判断是否画的正确.
解 A图没有指明正方向;
B图中,1和-1表示的一个单位长度不相等,在同一数轴上,单位长度必须一致;
C图中没有原点;
D图中三要素齐全.
∴A、B、C三个图画的都不是数轴,只有D图画的是数轴.
例2 在所给的数轴上画出表示下列各数的点:
![]()
![]()
分析 第一步画数轴,第二步在数轴上找出相对应的点,每个正有理数都可用数轴上原点右边的一个点来表示,例如2、3.5,可用数轴上分别位于原点右边2个单位,3.5个单位的点表示.每一个负有理数都可用数轴上原点左边的一个点来表示,

解
![]()
点评 数轴上表示数的点可用大写字母标出,写在数轴上方所对应数的上面,原点用O标出,它表示数0.数轴上原点的位置要根据需要来确定,不一定要居中.单位长度应根据需要来确定,1 cm的长度可以表示1个单位长度,也可以表示2个,5个,10个…单位长度,但在同一数轴上,单位长度必须一致,不可随意改变.
例3 指出数轴上A、B、C、D、E各点分别表示什么数.
![]()
分析

解
![]()
例4 下面说法中错误的是 [ ]
A.数轴上原点的位置是任意取的,不一定要居中;
B.数轴上单位长度的大小要根据实际需要选取.1厘米长的线段可以代表1个单位长度,也可以代表2个、5个、10个、100个、…单位长度,但一经取定,就不可改动;
C.如果a<b,那么在数轴上表示a的点比表示b的点距离原点更近;
D.所有的有理数都可以用数轴上的点表示,但不能说数轴上所有的点都表示有理数.
解 当a,b都是正数时,C的结论成立;
当a,b不都是正数时,例如a=-10,b=2,此时-10<2,也满足条件a<b,但表示a的点与原点的距离(10)比表示b的点与原点的距离(2)远,C的结论不成立.
∴C错.
点评 因为有理数包含正数、负数和0,所以用字母表示数时,这个字母就可以代表正数、负数或0.在分析问题时,忘记字母代表的数可能是负数或0经常是造成错误的原因.
例5 比较下列各组数的大小:

分析 依据“正数都大于0,负数都小于0;正数大于一切负数.”和“在数轴上表示的两个数,右边的数总比左边的数大.”比较两个数的大小.

解
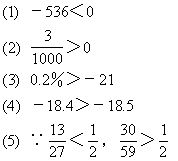
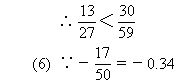
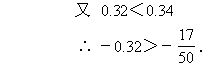
点评 分母不同的两个分数比较大小时,一般采用通分的方法.当分母比较大时,通分是比较麻烦的,这时应当考虑其他的方法和技巧.例如:借助中间数的方法;让分子相等比分母的方法,比较它们的倒数的方法等等.