 设为首页
设为首页
 加入收藏
加入收藏
典型例题
一、用平方差公式分解因式的题目(体会换元思想)
例1 把下列各式分解因式:
(1) ![]() ;
(2)
;
(2) ![]()
解:(1) ![]() 可以看作是
可以看作是 ![]() ,
, ![]() 可以看作是
可以看作是 ![]() ,则
,则
![]()
![]() ;
;
(2) ![]() 可以看作是
可以看作是 ![]() ,则
,则
![]()
![]()
点拨:(1)把 ![]() 看作是
看作是 ![]() 是逆用了幂的乘方公式
是逆用了幂的乘方公式 ![]() ,也就是运用了公式
,也就是运用了公式 ![]() ,而把
,而把 ![]() 看作
看作 ![]() ,
, ![]() 看作
看作 ![]() 是逆用了积的乘方公式
是逆用了积的乘方公式 ![]() ,而灵活运用公式是解题中所必须掌握的基本技巧。
,而灵活运用公式是解题中所必须掌握的基本技巧。
(2)平方差公式中的 ![]() 可以是数、字母或数与字母的乘积,在此进一步体现了换元思想的应用。
可以是数、字母或数与字母的乘积,在此进一步体现了换元思想的应用。
例2 把下列各式分解因式:
(1) ![]() ;
(2)
;
(2) ![]()
解:(1)把 ![]() 和
和 ![]() 分别看作平方差公式中的
分别看作平方差公式中的 ![]() 和
和 ![]() ,于是
,于是
![]()
![]()
![]() ;
;
(2)由于 ![]() ,
, ![]() ,所以
,所以 ![]() 和
和 ![]() 分别看作平方差公式中的
分别看作平方差公式中的 ![]() ,于是
,于是
![]()
![]()
![]()
点拨:利用换元思想,使平方差公式的使用范围更加广泛,公式中的 ![]() 不仅可以是单项式、多项式,也可以是单项式与多项式的乘积。
不仅可以是单项式、多项式,也可以是单项式与多项式的乘积。
例3 把下列各式分解因式:
(1) ![]() ;
(2)
;
(2) ![]() ;
;
分析:多项式中有公因式,先提出来。
解:(3) ![]()
![]() ;
;
(2) ![]()
![]()
![]()
点拨:(1)提取公因式后可使括号内的多项式化简,所以在对多项式进行因式分解时,提公因式是首先要进行的步骤;
(2)分解因式是在有理数范围内进行的,其结果是在有理数范围内不能再继续分解为止,如 ![]() ;
;
(3)有些多项式需多种方法,多个分解步骤才可完成分解,因此,第一要养成随时检查多项式能否再继续分解的解题习惯;第二要善于综合运用各种方法作因式分解,提高解题能力。
例4 已知 ![]() 和
和 ![]() 满足方程组
满足方程组 ![]() ,求代数式
,求代数式 ![]() 的值。
的值。
解法1:解方程 ![]() 得
得 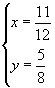
将 ![]() ,
, ![]() 代入
代入 ![]() 得
得
![]()
![]()
解法2: 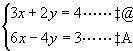
由②得
![]() ……③
……③
∴
![]()
![]()
![]()
点拨:解法一是最基本的方法,容易想到,但计算较繁。解法二利用了分解因式的知识,比较巧妙,但不容易想到。所以,要想解题又快又准,必须熟练掌握所学过的知识,提高综合运用知识的能力。
二、用完全平方公式分解因式的题目
例1 把下列各式分解因式:
(1) ![]() ;
(2)
;
(2) ![]()
(3) ![]()
解:(1)由于16可以看作 ![]() ,于是有
,于是有
![]()
![]() ;
;
(2)由幂的乘方公式, ![]() 可以看作
可以看作 ![]() ,
, ![]() 可以看作
可以看作 ![]() ,于是有
,于是有
![]()
![]() ;
;
(3)由积的乘方公式, ![]() 可以看作
可以看作 ![]() ,于是有
,于是有
![]()
![]()
![]()
![]()
点拨:(1)多项式具有如下特征时,可以运用完全平方公式作因式分解:①可以看成是关于某个字母的二次三项式;②其中有两项可以分别看作是两数的平方形式,且符号相同;③其余的一项恰是这两数乘积的2倍,或这两数乘积2倍的相反数。而结果是“和”的平方还是“差”的平方,取决于它的符号与平方项前的符号是否相同。
(2)在运用完全平方公式的过程中,再次体现换元思想的应用,可见换元思想是重要而且常用思想方法,要真正理解,学会运用。
例2 把下列各式分解因式:
(1) ![]() ;
(2)
;
(2) ![]()
解:(1)先将平方项的系数转化为正数,于是有
![]()
![]()
![]()
![]() ;
;
(2)先提出公因式6,于是有
![]()
![]()
![]()
![]()
![]()
![]()
点拨:(1)在使用完全平方公式时,要保证平方项前的符号为正,当平方项前的符号是负号时,先提出负号。
(2)多项式若有公因式,则先考虑提取,使多项式简化,以便观察分解策略。
例3 若 ![]() 是一个完全平方公式,那么
是一个完全平方公式,那么 ![]() 的值应该是(
)
的值应该是(
)
(A)8 (B)16 (C)-16 (D)16或-16
答(D)因为完全平方式是可以化为形如 ![]() 或
或 ![]() 的形式的多项式,故
的形式的多项式,故 ![]() 既然是完全平方式,就可将它化为
既然是完全平方式,就可将它化为 ![]() 或
或 ![]() ,将
,将 ![]() ,
, ![]() 展开与
展开与 ![]() 比较对应项系数可得
比较对应项系数可得 ![]() 或-16。
或-16。