第三节 垂直于弦的直径

典型例题

　　1、如图，已知⊙O的直径AB和弦CD相交于点E，AE=6cm，EB=2cm，∠BED=30°，求CD的长.

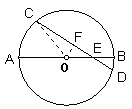
　　分析  要充分利用条件∠BED=30°，构造出以弦心距、半径、半弦组成的一个直角三角形，通过解直角三角形求得未知量.

　　解  过O作OF⊥CD于F，连结CO，

　　∵AE=6cm，EB=2cm，∴AB=8cm

　　∴OA=AB=4cm，OE=AE-AO=2cm，

　　在Rt△OEB中，∵∠CEA=∠BED=30°，

　　∴OF=OE=1cm.

　　在Rt△CFO中，OF =1cm，OC＝OA＝4cm，

　　∴CF=cm．

　　又∵OF⊥CD．∴ CD＝2CF＝2cm．

　　答：CD的长为2cm.

　　说明：此题是利用垂径定理的计算问题.在求有关弦心距、弦长和半径等问题时，常常利用弦心距和半径构成直角三角形求解；另外此题若直接利用以后的“相交弦定理”来解，较为困难.

　　2、已知：△ABC内接于⊙O，AB=AC，半径OB=5cm，圆心O到BC的距离为3cm，求AB的长．

　　分析：①此题没有图形，在解题时应考虑到满足条件的图形，此题有两种情况；②利用条件构造垂径定理的基本图形解题．

　　解：分两种情况：

　　

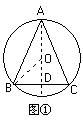
　　（1）如图①，过A作AD⊥BC于D，

　　又∵AB=AC，∴点O在AD上，∴OD=3cm．连结OB，

　　在Rt△ODB中，OB==5cm，OD=3cm，由勾股定理，得

　　，∴

　　在Rt△ADB中， AD=AO+OD=5+3=8cm，由勾股定理，得

　　，∴（cm）

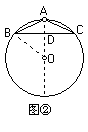
　　（2）如图②，同理可得：

　　AB=（cm）．

　　说明：①此题的目的主要是培养学生的严密性思维和解题方法：确定图形——分析图形——数形结合——解决问题；②作辅助线的能力．

　　3、在直径为50cm的⊙O中，弦AB=40cm，弦CD=48cm，且AB∥CD，求：AB与CD之间的距离.

　

　　分析：此题没有图形，在解题时应考虑到满足条件的两弦可能在圆心的同侧，也可能在在圆心的两侧，即有两解.

　　解：（略，8cm，22cm）

　　说明：此题的目的主要是培养学生的严密性思维和解题方法：确定图形——分析图形——数形结合——解决问题.

　　4、已知：如图，AB是⊙O的直径，CD是弦，AE⊥CD于E ，BF⊥CD于F .求证： CE=DF ；OE=OF

　

　　分析：本题的关键是作OH⊥CD，构造垂径定理的基本图形解题，另外还用到平行线等分线段定理等.

　　证明：（一）过O作OH⊥CD于H，

　　∵AE⊥CD，BF⊥CD  ∴AE∥OH∥BF

　　∵AO = BO   ∴EH = HF 

　　∵OH⊥CD且O为圆心∴CH = HD

　　∴CH－EH = HD－HF 即  CE = DF

　　∵EH = HF ，OH⊥EF  ∴ OH是EF的中垂线

　　∴ OE = OF  .

　　证明（二）延长EO交BF于G，用三角形全等和直角三角形斜边中线证明OE = OF.

　　说明：（1）此题展示构造垂径定理的基本图形解题的基本方法；（2）让几何动起来.引申：让弦CD动起来，与直径AB不相交，让学生在运动中观察、发现问题，培养学生的探究能力.

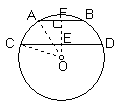
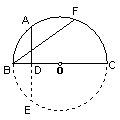
　　5、如图，F是以O为圆心，BC为直径的半圆上任意一点，A是 的中点，AD⊥BC于D，求证：AD= BF.

　　分析：（方法一）由于A是 的中点，连结OA可构造垂径定理的基本图形，BE=BF，△ADO≌△BEO，得AD=BE=BF.

　　（方法二）如图，补圆，延长AD交⊙O于E，造垂径定理的基本图形，问题即可解决.

　　证明：（略）

　　说明：此题是垂径定理的应用为过程，培养学生的发散思维.

返回页首