第五节 圆周角

典型例题

　　例1 在半径等于5cm的圆内有长为5cm的弦，则此弦所对的圆周角为（ ）．

　　（A）60°或120°　（B）30°或120°　（C）60°　（D）120°

　　解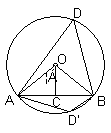：如图， OA＝OB＝5cm，AB＝5cm．过O作OC上AB于C，

　　则AC=cm．∵sinα=  

　　∵α为锐角，∴α=60°．∴∠AOB=120°．

　　当圆周角的顶点在优弧 上时，得∠ADB=60°；当圆周角的顶点在劣弧 上时．得∠AD’B＝120°．

　　∴此弦所对的圆周角为60°或120°．

　　说明：此题为基础题，求一条弦所对的圆周角．圆周角的顶点可以在这条弦所对的优孤上，也可以这这条弦所对的劣弧上．

　　例2、（河南省，2002）已知：如图，以△ABC的BC边为直径的半圆交AB于D，交AC于E，过E作EF⊥BC，垂足为F，且BF:FC=5:1，AB=8，AE=2．求EC的长．

　　分析：连结BE，构造直角三角形，并出现典型的双垂直图形，通过解直角三角形解得．

　　解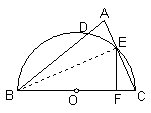：如图，连结BE，则BE⊥AC，

　　∴，

　　设BF=5x，BC=6x．

　　∵EF⊥BC，∠EBF=∠CBE，

　　∴△BEF∽△BCE，∴．即60=5x·6x，∵FC>0，∴．

　　∴，∵，∴．

　　说明：①添加辅助线，构造直角三角形；②构成典型的双垂直图形，非常重要．

　　例3、（陕西省，2002）已知：如图，BC为半圆O的直径，F是半圆上异于B、C的一点，A是 的中点，AD⊥BC于点D，BF交AD于点E．

　　（1）求证：BE·BF=BD·BC；

　　（2）试比较线段BD与AE的大小，并说明道理．

　　分析：（1）连结FC，证△BDE∽△BCF即可；（2）要比较两条线段的大小，通常是把两条线段转移到一个三角形内，利用大角对大边来判断．

　　证明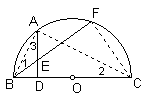：（1）连结FC，则BF⊥FC．

　　在△BDE和△BCF中，

　　∵∠BEC=∠EDB=90°，∠EBC=∠EBD，∴△BDE∽△BCF．

　　∴，即BE·BF=BD·BC．

　　解：（2）AE>BD，连结AC、AB，则∠BAC=90°，∵ = ，∴∠1=∠2．

　　又∵∠2+∠ABC=90°，∠3+∠ABD=90°，∴∠2=∠3，∴AE=BE．

　　在Rt△EBD中，BE>BD，∴AE>BD．

　　说明：①训练学生添加辅助线；②第（2）小问是教材P102中3题的拓展．

　　例4、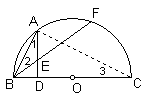（太原市，2002）如图，已知BC为⊙O的直径，AD⊥BC，垂足为D，BF交AD于E，且AE=BF．

　　（1）求证： = ；

　　（2）如果sin∠FBC=，AB，求AD的长．

　　解：（1）连结AC．∵BC是⊙O的直径，∴∠BAC=90°，

　　又AD⊥BC，垂足为D，∴∠1=∠3．

　　在△AEB中，AE=BE，∴∠1=∠2．∴∠2=∠3， = ．

　　（2）设DE=3x，∵AD⊥BC，sin∠FBC=，∴BE=5x，BD=4x．

　　∵AE=BE，∴AE=5x，AD=8x．

　　在Rt△ADB中，∠ADB=90°，AB，∴．

　　解这个方程，得 x=1，∴AD=8．

　　说明：①此题是教材P102中3题的变形；②训练学生求线段长度的方法：直接求和列方程求解．

返回页首