第二十一节 圆柱和圆锥的侧面展开图

典型例题

　　例1 （1）若圆锥的底面半径是3cm，母线长是5cm，则它的侧面展开图的面积是 .

　　（2）若圆锥的母线长为5cm，高为3cm，则其侧面展开图中扇形的圆心角是_______度.

　　分析 首先弄清圆的侧面展开图是扇形，（1）中可直接用 求得 ，（2）中先求底面圆半径，扇形弧长，再由弧长公式求圆内角为288°.

　　例2 （1）如果圆柱底面半径为4cm，它的侧面积为 ，那么圆柱的母线长为（　）.

　　（A）16cm　（B）16 cm　（C）8cm　（D）8 cm

　　（2）如果圆柱底面直径为6cm，母线长为10cm，那么圆柱的侧面积为（　）

　　（A）30 　（B）60 　（C）90 　（D）120

　　分析 圆柱侧面展开图是矩形，（1）可直接用公式求出母线长为8cm，故选（C），（2）中，由直径求出半径是关键，应选（B）.

　　例3 一个圆锥的高是10㎝，侧面展开图是半圆，求圆锥的侧面积.

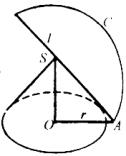　　 分析：如图，欲求圆锥的侧面积，即求母线长l，底面半径r.由圆锥的形成过程可知，圆锥的高、母线和底面半径构成直角三角形即 ，且 关键找出l与r的关系，又其侧面展开图是半圆，可得关系 ，即 .

　　解：设圆锥底面半径r，扇形弧长为C，母线长为l，

　　由题意得 又

　　 得 　　　①

　　在 中， 　②

　　由①、②得：

　　∴所求圆锥的侧面积为

　　

　　例4 圆锥的轴截面是等腰 ，EG 是AB上一点，且 ，那么在锥面上A、M两点间的最短距离是多少？

　　分析：设圆锥的侧面展开图是扇形 A点落在 点，则所求 、M之间的最短距离就是侧面展开图中线段 M的长度.

　　解：如图，扇形的圆心角

　　 ，在 中，过 作 于N，则

　　

　　 中，

返回页首