第四节 不等式的解法举例

例1 解不等式：（1） ；
　　　　　　　（2） ．

　　分析 如果多项式 可分解为 个一次式的积，则一元高次不等式 （或 ）可用“穿根法”求解，但要注意处理好有重根的情况．

　　解 （1）原不等式可化为



　　把方程 的三个根 顺次标上数轴．然后从右上开始画线顺次经过三个根，其解集如下图的阴影部分．

　　∴原不等式解集为

　　（2）原不等式等价于



　　∴原不等式解集为

　　说明 用“穿根法”解不等式时应注意：①各一次项中 的系数必为正；②对于偶次或奇次重根可转化为不含重根的不等式，也可直接用“穿根法”，但注意“奇穿偶不穿”，其法如下图．

例2 解下列分式不等式：

　　（1） ；  （2）

　　分析 当分式不等式化为 时，要注意它的等价变形

　　①

　　②

　　（1）解 原不等式等价于



用“穿根法”

　　∴原不等式解集为 。

　　（2）解法一 原不等式等价于



　　∴原不等式解集为 。

解法二 原不等式等价于



　　用“穿根法”

　　∴原不等式解集为

例3 解不等式

　　分析 解此题的关键是去绝对值符号，而去绝对值符号有两种方法：一是根据绝对值的意义

　　二是根据绝对值的性质： 或 ，因此本题有如下两种解法．

解法一 原不等式

　　即

　　∴ 或

　　故原不等式的解集为 ．

解法二 原不等式等价于

　　即 ∴ ．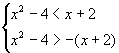

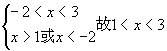返回顶部