第六节 抛物线的几何性质

典型例题（例1～例4）

　　例1 如图所示，过抛物线焦点的一条直线与它交于两点P、Q，通过点P和抛物线顶点的直线交准线于点M，如何证明直线MQ平行于抛物线的对称轴？

　　解：思路一：求出M、Q的纵坐标并进行比较，如果相等，则MQ//x轴，为此，将方程  联立，解出



　　直线OP的方程为 即

　　令 ，得M点纵坐标 得证．

　　由此可见，按这一思路去证，运算较为繁琐．

　　思路二：利用命题“如果过抛物线 的焦点的一条直线和这条抛物线相交，两上交点的纵坐标为 、 ，那么 ”来证．

　　设 、 、 ，并从 及 中消去x，得到 ，则有结论 ，即 ．

　　又直线OP的方程为 ，含 ，得 ．

　　因为 在抛物线上，所以 ．

　　从而 ．

　　这一证法运算最较小．

　　思路三：直线MQ的方程为 的充要条件是 ．

　　将直线MO的方程 和直线QF的方程 联立，它的解（x ,y）就是点P的坐标，消去 的充要条件是点P在抛物线上，得证．这一证法巧用了充要条件来进行逆向思维，运算量也较小．

　　注：本题中过抛物线焦点的直线与x轴垂直时（即余率不存在），容易证明成立．

　　例2 已知过抛物线 的焦点且斜率为1的直线交抛物线于A、B两点，点R是含抛物线顶点O的弧AB上一点，求△RAB的最大面积．

　　分析；求RAB的最大面积，因过焦点且斜率为1的弦长为定值，故可以 为三角形的底，保要确定高的最大值即可．

　　解：设AB所在的直线方程为 ．

　　将其他入抛物线路 ，得



　　当过R的直线l平行于AB且与抛物线相切时，△RAB的面积有最大值．

　　设直线l方程为 ．代入抛物线方程得

　　由 得 ，这时 ．它到AB的距离为

　　∴△RAB的最大面积为 ．

　　例3 直线 过点 ，与抛物线 交于 、 两点，P是线段 、 的中点，直线 过P和抛物线的焦点F，设直线 的斜率为k．

　　（1）将直线 的斜率与直线 的斜率之比表示为k的函数 ；

　　（2）求出 的定义域及单调区间．

　　分析： 过点P及F，利用两点的斜率分，可将 的斜率用k表示出来，从而写出 ，由函数 的特点求得其定义域及单调区间．

　　解：（1）设 的方程为： ，将它代入方程 ，得

　　设 ，则

　　将 代入 得： ，即P点坐标为 ．

　　由 ，知焦点 ，∴直线 的斜率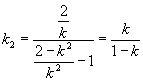

　　∴函数 ．

　　（2）∵ 与抛物线有两上交点，∴ 且

　　解得 或

　　∴函数 的定义域为

　　当 时， 为增函数．

　　例4 如图所示：直线l过抛物线 的焦点，并且与这抛物线相交于A、B两点，求证：对于这抛物线的任何给定的一条弦CD，直线l不是CD的垂直平分线．

　　分析：本题所要证的命题结论是否定形式，一方面可根据垂直且平分列方程得矛盾结论；别一方面也可以根据l上任一点到C、D距离相等来得矛盾结论．

　　证法一：假设直线l是抛物线的弦CD的垂直平方线，因为直线l与抛物线交于A、B两点，所以直线l的斜率存在，且不为零；直线CD的斜率存在，且不为0．

　　设C、D的坐标分别为 与 ．则

　　∴l的方程为

　　∵直线l平分弦CD

　　∴CD的中点 在直线l上，

　　即 ，化简得：

　　由 知 得到矛盾，所以直线l不可能是抛物线的弦CD的垂直平分线．

　　证法二：假设直线l是弦CD的垂直平分线

　　∵焦点F在直线l上，∴

　　由抛物线定义， 到抛物线的准线 的距离相等．

　　∵ ，

　　∴CD的垂直平分线l： 与直线l的抛物线有两上交点矛盾，下略．

典型例题（例5～例7）

　　例5 设过抛物线 的顶点O的两弦OA、OB互相垂直，求抛物线顶点O在AB上射影N的轨迹方程．

　　分析：求与抛物线有关的轨迹方程，可先把N看成定点 ；待求得 的关系后再用动点坐标 来表示，也可结合几何知识，通过巧妙替换，简化运算．

　　解法一：设

　　则： ，

 ， 即



 ，                            ①

　　把N点看作定点，则AB所在的直线方程为： 显然

 代入 化简整理得：

 ，                      ②

　　由①、②得： ，化简得

　　用x、y分虽表示 得：

　　解法二：点N在以OA、OB为直径的两圆的交点（非原点）的轨迹上，设 ，则以OA为直径的圆方程为：

                   ①

　　设 ，OA⊥OB，则

　　在求以OB为直径的圆方程时以 代 ，可得

                    ②

　　由①＋②得：



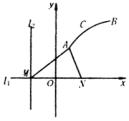　　例6　如图所示，直线 和 相交于点M， ⊥ ，点 ，以A、B为端点的曲线段C上的任一点到 的距离与到点N的距离相等，若△AMN为锐角三角形， ， ，且 ，建立适当的坐标系，求曲线段C的方程．

分析：因为曲线段C上的任一点到 为准线的抛物线的一段，所以本题关键是建立适当坐标系，确定C所满足的抛物线方程．

　　解： 为x轴，MN的中点为坐标原点O，建立直角坐标系．

　　由题意，曲线段C是N为焦点，以 为准线的抛物线的一段，其中A、B分别为曲线段的两上端点．

　　∴设曲线段C满足的抛物线方程为： 其中 、 为A、B的横坐标

令 则 ，

　　∴由两点间的距离公式，得方程组：

　　解得 或

　　∵△AMN为锐角三角形，∴ ，则 ，

　　又B在曲线段C上，

　　则曲线段C的方程为

　例7　如图所示，设抛物线 与圆 在x轴上方的交点为A、B，与圆 在x由上方的交点为C、D，P为AB中点，Q为CD的中点．

　　（1）求 ．（2）求△ABQ面积的最大值．

　　分析：由于P、Q均为弦AB、CD的中点，故可用韦达定理表示出P、Q两点坐标，由两点距离公式即可求出 ．

　　解：（1）设

　　由 得： ，





　　由 得 ，





　　同 类似，

　　则 ，

　　（2）



 ，∴当 时， 取最大值 ．