 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
使物体带电有三种方法
1、接触带电.将不带电体与带电体接触,则不带电体带了电.接触带电的特点是带同性电荷,但所带电量不一定与带电体电量相等.如果导体完全相同,接触后各带一半电量(不同的导体接触,电量的分配应按各自电容量的大小分配).
2、摩擦带电.初中已学过,这种带电特点是相互摩擦的两物体分别带有等量异种电荷.
3、静电感应带电.当不带电导体靠近带电体时,由于静电感应,在该导体两端产生等量异种电荷.若将该导体接地后又断开(或用手触摸一下随即将手离开),则该导体带上异种电荷.这便是感应带电的特点.
扩展资料
带同种电荷的物体也可以相互吸引
C· ![]() ·福里斯,A·B·季莫列娃所著的世界名著《普通物理学》第二卷第一分册(1979)第3页中说:“带同号电荷的物体(例如都带正电荷)互相排斥;带异号电荷的物体则互相吸引”.仔细研究可以发现这种说法欠妥.只有当带电体纯属点电荷时,说法才正确,除此之外,情况就不是这么简单,应具体问题作具体分析.
·福里斯,A·B·季莫列娃所著的世界名著《普通物理学》第二卷第一分册(1979)第3页中说:“带同号电荷的物体(例如都带正电荷)互相排斥;带异号电荷的物体则互相吸引”.仔细研究可以发现这种说法欠妥.只有当带电体纯属点电荷时,说法才正确,除此之外,情况就不是这么简单,应具体问题作具体分析.
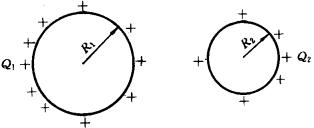
如图所示,两个带电的金属球,它们的半径各为 ![]() 与
与 ![]() ,所带的电量分别为
,所带的电量分别为 ![]() 和
和 ![]() .如果
.如果 ![]() 和
和 ![]() 同号,两个金属球之间的作用力一定是排斥的吗?要知道,这里的情况和两个点电荷情况不同,因为有感应电荷出现,情况比较复杂,答案必须根据具体情况进行分析计算.结论如下:
同号,两个金属球之间的作用力一定是排斥的吗?要知道,这里的情况和两个点电荷情况不同,因为有感应电荷出现,情况比较复杂,答案必须根据具体情况进行分析计算.结论如下:
(1)若当 ![]() 与
与 ![]() 等量同号,且
等量同号,且 ![]() ,则两球之间始终表现为斥力.
,则两球之间始终表现为斥力.
(2)若 ![]() 与
与 ![]() 异量同号,且
异量同号,且 ![]() ,则在相距较远时,两球可当作点电荷,它们之间是斥力.当两球相距较近或所带电量差别悬殊时,由于感应的影响,一部分球面上的斥力与另一部分球面上的吸引力可能互相抵消,也可能吸引力大于斥力,以致彼此相吸引!
,则在相距较远时,两球可当作点电荷,它们之间是斥力.当两球相距较近或所带电量差别悬殊时,由于感应的影响,一部分球面上的斥力与另一部分球面上的吸引力可能互相抵消,也可能吸引力大于斥力,以致彼此相吸引!
对于上述结论,为避免冗长烦琐地数学计算,我们仍采用电力线性质定性加以证明.
我们先讨论两球带等量同号电荷的情况.在“电力线及其应用”一节中,我们将会征得如下结论:“两个导体中(不论电荷量如何),至少有一个导体其表面上各点的面电荷密度不会异号.”但由于两球半径相等,电量相等,电势也总是相等,依对称性又不能出现一个球上仍保持表面各点的电荷面密度同号,而另一个球上出现异号的情况.据此,当两球距离变化时,电荷面密度只能在同号电荷范围内变化,作用力是斥力的性质保持不变.
其次,我们讨论两球带异量同号电荷且球半径不等的情况.为确定起见,假定两球原来带的是正电荷(若是负电荷可同样论证),根据与上面类似的讨论可以肯定,两球中至少有一球(带电量多的球面上不会出现异号电荷,否则会导致矛盾的结果).若两球的带电量相差不大,相距又较远,则带电量小的球面上也不会感应出异号电荷.这时,两球的电势虽不相等,但不会有起始于一个球面而终止于另一球面的电力线,因此它们之间的相互作用力是排斥力.当两球的带电量的差别增大到一定程度,两球距离较近时.带电量小的球面上会感应出异号电荷,这时开始有部分电力线起始于一个球面而终止于另一个球面,两球面上与此相关的电荷之间存在着吸引作用;但其余的大部分电力线仍分别是从两球面发出(相应于球面带正电荷)而终止于无穷远或起始于无穷远而终止于球面(相应于球面带负电荷),两球面上与此相关的电荷之间存在着排斥作用.总的效果仍表现为排斥力.随着两球电量的差异的不断增大,或两球间距不断减小,相互间的排斥力也不断减小,可以想象,当达到 某一临界态时,合力刚好为零,即在这种情况下,两球之间没有力的作用.很明显,若再进一步增大两球带电量的差别或缩短两球的间距,则它们之间就会产生吸引力.
为了更进一步说明问题,我们再举一个能定量讨论的例子.
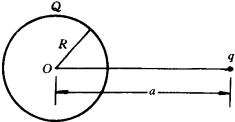
设有一个半径为R的金属球,带有电荷Q,距球心O为a(a>R)的地方再放置一个点电荷q,如图所示.Q与q是同种电荷(例如都是正电荷),则根据电像法,不难求出这时q与金属球上电荷之间的相互作用力为:
 (1)
(1)
显然F>0时相互排斥, ![]() 时相互吸引.由(1)式可见,当:
时相互吸引.由(1)式可见,当:
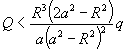 (2)
(2)
时,q与金属球便会相互吸引,具体可在下列情况下出现.
(1)Q很小.对于给定的q、R、a而言,只要Q足够小,(2)式总是可以满足的.从物理本质上看,如果Q=0,即金属球原来不带电,则在q出现后,球面上便会产生感应电荷,靠近q那侧球面总是出现与q相反的负电荷,远离q那侧球面总是出现与q相同的正电荷.因此球上负电荷吸引q的力便大于球上正电荷排斥q的力,结果q受整个球上电荷的作用力总是吸引力.如果再把Q(正电荷)放在球上,则不管怎样分布,Q作用在q上的力总是排斥力,但当Q足够小,以致于排斥力小于感应电荷对q的吸引力时,q受到球上电荷总的作用力便仍然是吸引力.
(2)(a-R)很小(即q离球面很近).这时.接近R,故(2)式右边分母很小,因而(2)式同样可以满足.从物理本质上看,这时q很靠近球面,在球面上感应出来的负电荷很多,因而吸引力就很大.所以只要q离金属球足够近,则q与球上电荷之间的作用力就总是吸引力.
扩展资料
为什么两条电场线不能相切?
 在电场的教学中,我们在讲解两条电场线为什么不能相交时,一般都采取教参中的说法,即如果两条电场线相交,则在交点处电场强度的方向有两个,分别为两条电场线在此点的切线方向,如图1所示.这显然是不可能的,所以两条电场线不能相交.这种解释条理非常清楚,学生易于接受.但这种解释有一个缺陷,那就是不能说明两条电场线为什么不能相切.在如图2所示情形中,A、B两条电场线相切于P点,如果用上述说法来解释,则A、B两条电场线的切线方向可能为同一条方向,即C所指方向,这样,在切点P处的电场强度方向也就只有一个.显然,上述说法不能解释两条电场线为什么不能相切,教参对此也没有说明.我们在教学过程中也很容易忽视这一点,学生根据上述解释,就很容易得出两条电场线可以相切的错误结论.
在电场的教学中,我们在讲解两条电场线为什么不能相交时,一般都采取教参中的说法,即如果两条电场线相交,则在交点处电场强度的方向有两个,分别为两条电场线在此点的切线方向,如图1所示.这显然是不可能的,所以两条电场线不能相交.这种解释条理非常清楚,学生易于接受.但这种解释有一个缺陷,那就是不能说明两条电场线为什么不能相切.在如图2所示情形中,A、B两条电场线相切于P点,如果用上述说法来解释,则A、B两条电场线的切线方向可能为同一条方向,即C所指方向,这样,在切点P处的电场强度方向也就只有一个.显然,上述说法不能解释两条电场线为什么不能相切,教参对此也没有说明.我们在教学过程中也很容易忽视这一点,学生根据上述解释,就很容易得出两条电场线可以相切的错误结论.
那我们应该怎样来解释两条电场线为什么不能相切呢?
 为了使电场线不仅能描写场强方向也能描写场强大小,我们引入电场线密度的概念.在电场中任一点取一小面元
为了使电场线不仅能描写场强方向也能描写场强大小,我们引入电场线密度的概念.在电场中任一点取一小面元 ![]() 与该点场强方向垂直,设穿过
与该点场强方向垂直,设穿过 ![]() 的电场线有
的电场线有 ![]() 根,则比值
根,则比值 ![]() 叫做该点电场线密度,它的意义是通过该点单位垂直截面的电场线根数.在作电场线图时,我们总是使电场中任一点的电场线密度与该点场强大小成正比,即
叫做该点电场线密度,它的意义是通过该点单位垂直截面的电场线根数.在作电场线图时,我们总是使电场中任一点的电场线密度与该点场强大小成正比,即 ![]() ,这样电场线密的地方电场强度大,电场线稀的地方电场强度小.如图3所示,由电场线的性质有a处电场强度比b处大.从图2可知,越靠近切点P,
,这样电场线密的地方电场强度大,电场线稀的地方电场强度小.如图3所示,由电场线的性质有a处电场强度比b处大.从图2可知,越靠近切点P, ![]() 越趋近于零,
越趋近于零, ![]() 有限,
有限, ![]() 的极限为无穷大,则在切点P,E为无穷大,这显然是不可能的,这就是两条电场线为什么不能相切的原因.在教学过程中可以这样来进行,在图2中,A与B两条电场线越靠近切点P,可以认为电场线越来越密,电场强度越来越大;在切点P,电场线密度为无穷大,即电场强度无穷大,这是不可能的,所以两条电场线不能相切.这样进行解释,学生易于接受.讲完这一点后,紧接着进行总结:两条电场线为什么不能相交是用到了电场线的一个性质,即电场强度的方向沿电场线的切线方向.而解释两条电场线为什么不能相切则用到了电场线的另一性质,即电场线的密部场强大、电场线的疏部场强小.
的极限为无穷大,则在切点P,E为无穷大,这显然是不可能的,这就是两条电场线为什么不能相切的原因.在教学过程中可以这样来进行,在图2中,A与B两条电场线越靠近切点P,可以认为电场线越来越密,电场强度越来越大;在切点P,电场线密度为无穷大,即电场强度无穷大,这是不可能的,所以两条电场线不能相切.这样进行解释,学生易于接受.讲完这一点后,紧接着进行总结:两条电场线为什么不能相交是用到了电场线的一个性质,即电场强度的方向沿电场线的切线方向.而解释两条电场线为什么不能相切则用到了电场线的另一性质,即电场线的密部场强大、电场线的疏部场强小.