 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
绝对值中的数学思想
天津 肖泰来
绝对值的概念是中学数学中一个重要概念,它的应用十分广泛.因此我们在学习时,不仅应该深入理解概念,灵活运用,还应注意在应用过程中学会思想方法.
1.整体代换
例1若|a-2|=2-a,求a的取值范围.
解 根据已知条件等式的结构特征,我们把a-2看作一个整体,那么原式变形为|a-2|=-(a-2),又由绝对值概念知a-2≤0,故a的取值范围是a≤2.
2.数形结合
例2 已知a<0<c,ab>0,|b|>|c|>|a|,化简|a+c|+|b+c|-|a-b|.
解 分析这个题目的关键是确定a+c、b+c、a-b的符号,根据已知可在数轴上标出a、b、c的大致位置,如图所示:
![]()
很容易确定a+c>0,b+c<0,a-b>0,由绝对值的概念,原式=(a+c)-(b+c)-(a-b)=a+c-b-c-a+b=0.
用数轴上的点来表示有理数,用这样的点与原点的距离来表示有理数的绝对值,这里运用了数形结合的思想.
3.分类
例3五个有理数a、b、c、d、e满足|abcde|=-abcde,
![]()
解 由题设条件知,abcde<0,而 a、b、c、d、e满足abcde < 0仅有三种情况:①二正三负;②四正一负;③五负.又因为对于任意非零有理数a,有
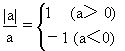
![]()
4.特殊化
有些数学题目,直接解原题时感到难以入手,可以先考察它的某些简单特例,而后达到解决原题的目的,这种思考问题的过程,称为“特殊化”方法.
例4 已知a、b是有理数,且a·b<0,试比较|a+b|,|a-b|,|a|+|b| ,||a|-|b||的大小.
解 根据已知a·b<0,不妨取a=1,b=-1,这样有|a+b|=0,|a-b|=2,|a|+|b|=2,||a|-|b||=0,
∴|a+b|=||a|-|b||<|a-b|
=|a|+|b|.
和初一同学谈谈怎样学好代数
湖北省钟祥市双河一中 周识贤
初一同学由学习算术进入学习代数,总觉得不适应.不少人还会产生困难,原因是什么呢?
1.中学的教学要求高了,小学阶段主要以培养运算能力为重点,而中学随着学生理解能力的提高,要逐步加强逻辑思维能力的训练与培养.
2.由于教学方法上的差异和学习环境的变化,不能迅速适应中学的教学秩序和教学规律
3.同算术相比,代数与算术在内容和方法上既有联系又有很大区别.
这些都是学习代数的不利因素,处理不好还会引起成绩“滑坡”.因此,要想比较自然地完成从小学到中学的过渡,应从三个方面去努力.
一、透彻理解新概念
比如学习有理数,首先遇到的是对一些新概念的理解.如相反数、绝对值等.
教材中说:“在一个数的前面添上‘-’号,就成为原数的相反数.”这里要认识两点:(1)互为相反数的含义;(2)添上负号的数就成为原数的相反数,但这个添上负号的数不一定就是负数.由此可知,一个数的相反数的相反数就是原数.
“绝对值”既是重点又是难点,学习时要充分予以重视.教材中对绝对值作了两次叙述:“一个数的绝对值是数轴上表示它的点到原点的距离”,“正数和零的绝对值是它本身,负数的绝对值是它的相反数.”前段话表示了“绝对值”的几何意义,是说一个数的绝对值是“非负数”,也就是说绝对值具有“非负性”的特点;后段话是说求某数的绝对值所得到的结果和原数间的关系.从而告诉了我们求绝对值的方法.
这样,我们既理解了绝对值的含义,又掌握了绝对值的求法,学起来就不感到困难了.
例 求|+3|,|-3.5|.
解 |+3|=3;|-3.5|=-(-3.5)=3.5
二、以新带旧,新旧对比
初一代数从根本上来说,是要解决好有理数、式的计算.由小学的算术数扩充到有理数,这是认识的一次飞跃.因此,要注意新旧对比,找出它们的区别与联系.算术中的四则运算是学习有理数四则运算的基础;但代数又是算术的发展,它们是有区别的.例如,在算术中减法不是都能实施的,但在有理数中就可以;算术中两个数之和一定大于其中一个加数,但在有理数中结论就不一定成立;算术只限于对具体的已知数进行计算,不允许未知数参加运算,而在代数中,未知数和已知数有着同样的权利,都是运算对象.
三、经常看书复习,培养自学能力
读数学书要看、想、练相结合,对新概念要逐字逐句领会,对前后知识要加以比较,注意区别与联系,对公式、法则要熟记,反复练习运用,注意总结规律.一定要克服不肯看书,不会看书的现象.中学阶段越来越多的知识要通过自觉的预习和复习来掌握和巩固.