 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
关于(a+b)2的推广
对于公式(a+b)2=a2+2ab+b2,可以从两方面推广:一是从指数推广;一是从项数推广.
我们知道,
(a+b)2=a2+2ab+b2. ①
由多项式的乘法,可以得到
(a+b)3=(a+b)2(a+b)
=(a2+2ab+b2)(a+b)
=a3+2a2b+ab2+a2b+2ab2+b3
=a3+3a2b+3ab2+b3. ②
从展开式①,②中,可以看出如下规律:
项数与次数
项数比次数多1;
展开式中的字母a按降幂排列,第一项的字母a的指数就是二项式的次数;而字母b则按升幂排列,末项b的指数也是二项式的次数;
各项中a,b指数的和都等于二项式的次数.
系数
首末两项的系数都是1;
②式中第二项的系数是①式中第一、二项系数的和;
②式中第三项的系数是①式中第二、三项系数的和.
上述规律,从下面的表中可以很清楚地展示出来.
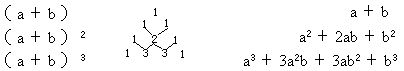
按上述规律,
(a+b)4
展开式各项的系数为
1 4 6 4 1
再结合项数与次数的规律,可得
(a+b4)=a4+4a3b+6a2b2+4ab3+b4. ③
由多项式的乘法验证,③的结果是对的.
事实上,由③可以推出(a+b)5展开式各项的系数,等等.当二项式的次数不大时,我们利用项数与次数以及系数的规律可以将展开式写出来.例如
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
如果你有兴趣,不妨按照上述规律写出(a+b)6的展开式.
上述二项式展开式的系数表在我国宋朝数学家杨辉著《详解九章算法》(1261年)一书中用过.杨辉在注释中提到,贾宪也用过上述办法.因此,我们称上述系数表为杨辉三角或贾宪三角.
下面看一看(a+b)2项数推广的情形.
我们用语言表述公式
(a+b)2=a2+2ab+b2 ①
为:两数和的平方,等于这两个数的平方和,加上这两个数积的2倍.
我们曾用多项式的乘法计算,得
(a+b+c)2=a2+b2+c2+2ab+2bc+2ac. ②
上式同样可用语言表述为:三数和的平方,等于这三个数的平方和,加上这三个数中每两个数的积的2倍.下面,我们用多项式的乘法计算四数和的平方.
(a+b+c+d)2=[(a+b)+(c+d)]2
=(a+b)2+2(a+b)(c+d)+(c+d)2
=a2+2ab+b2+2ac+2ad+2bc+2bd+c2+2cd+d2
=a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd. ③
同样,上式用语言表述为:四数和的平方,等于这四个数的平方和,加上这四个数中每两个数的积的2倍.
同学们如有兴趣,可利用公式②,③计算下列各题:
1.(a+2b-c)2.
2.(2x-y+3z)2.
3.(a+b-c-d)2.
4.(x-2y-z+2w)2.