第八节 同底数幂的除法

扩展资料

　　1．运用同底数幂的除法性质时应注意的问题是什么？

　　（1）运用法则的关键是看底数是否相同，而指数相减的是指被除式的指数减去除式的指数；

　　（2）因为零不能作除数，所以底数 ，这是此性质成立的先决条件；

　　（3）注意指数“1”的情况，如 ，不能把 的指数当做0；

　　（4）多个同底数幂相除时，应按顺序计算.

　　例 计算：

　　（1） ；

　　（2） ；

　　（3） ；

　　（4） .

　　思路启迪：这些题都可运用同底数幂除法的性质进行计算，其中第（2）题需先将 变为 ，从而转化为同底数幂的除数，第（3）题中两个幂的底数都是多项式 ；第（4）题要先进行幂的乘方运算，再进行同底数幂的除法计算，并且要注意运算顺序.

　　规范解法 （1）原式 ；

　　（2）原式 ；

　　（3）原式 ；

　　（4）原式 .

　　注：底数符号不同时，先确定符号，化成底数相同的形式，再运用同底数幂除法性质进行计算；第（4）题的过程中，要避免出现“ ”的错误.

　　2．应用零指数与负整数的意义时应注意的问题是什么？

　　（1）零指数幂和负整数指数幂中，底数都不能为0，即 .

　　（2）规定了零指数和负整数指数的意义后，正整数指数幂的运算性质就可以推广到整数指数幂.如 ， 等等.

　　例1 计算：

　　（1） ；　　　　（2） ；

　　（3） 　　　　（4） ；

　　（5） .

　　思路启迪：此例题是负整数指数幂和零指数幂的计算，根据 （ 是正整数， ）和 （ ）计算.

　　规范解法（1） ；

　　（2） ；

　　（3） ；

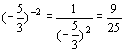　　（4）∵ ，∴ ，∴ ；

　　（5） .

　　例2 计算 .

　　规范解法 原式 .

　　注 （ ， 是正整数），这个结论在解题过程中可以直接用.

　　3．如何用科学计数法表示绝对值较小的数？

　　根据需要可以将一个绝对值较小的数表示成 （ ， 为负整数）的形式.其规律如下： 为该数第一个非零数字前面所有零的个数（包括小数点前面的那个零）.

　　例 用科学计数法表示下列各数：

　　（1） ；　　　（2） .

　　规范解法 （1） ；

　　（2） .

　　注 用科学记数法表示数 ，一般有两种类型：一种是 ，表示后， 为非负整数；另一种是 ，表示后， 为负整数.要熟记 的确定方法和规律.

　　4．为什么会出现负指数呢？

　　同底数幂除法性质为 （ ），那么对于 可视作 ，即 表示的是 ，同样 ， ， ，等等.所以负指数幂的形式可与分数之间相互转换.因此有 （ ， 是正整数）.

返回页首