第二十一节 圆柱和圆锥的侧面展开图

扩展资料

怎样应用圆柱和圆锥的侧面展开图解题？

　　答：圆柱和圆锥都是旋转体，它们的侧面都是曲面，又都是可展的曲面，即它们都可以展开铺在平面上．

　　如图1所示，圆柱的侧面展开图是矩形，这个矩形的一边长等于圆柱的高，即圆柱的母线长，另一边长是圆柱底面圆的周长；圆锥的侧面展开图是一个扇形，这个扇形的半径是圆锥的母线，弧长是圆锥底面圆的周长．

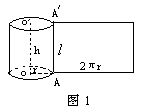
　　我们知道，圆柱、圆锥侧面展开图的面积就是它们的侧面积．如果用l表示圆柱或圆锥的母线长，用r表示它们底面的半径，由上面的分析可知：

　　圆柱侧面积=2πrl，

　　圆锥侧面积=πrl．

　　这里应用了矩形与扇形的面积公式．

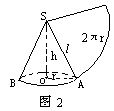
　　圆锥侧面展开图扇形的圆心角的θ°，由于扇形的弧长等于圆锥底面的周长，即有

　　所以

　　利用圆柱和圆锥侧面展开图，可以求得它们的侧面积，这是表面积的一部分．显然，圆柱的表面积还应加上两个底面面积，圆锥的表面积则需加上一个底面面积．

　　圆柱、圆锥的侧面展开图不仅用于表面积的计算．工厂的工人师傅要制造各种圆柱、圆锥的工件时，常常要根据工件的尺寸，通过计算，在材料板上画出下料图，然后再裁下制作．所以，展开图的知识在生产实际中也是很有用的．

　　[例1] 将半径为30厘米的薄铁圆板沿三条半径截成全等的三个扇形，做成三个圆锥筒(无底)．求圆锥筒的高(不计接头)．

　　解：依题意每个扇形的圆心角为120°，圆锥筒母线长l=30厘米．

　　设圆锥底面半径为rcm，则有

　　　

　　所以

　　　

　　

　　答：圆锥筒的高约为28.3厘米．

　　圆柱和圆锥都是空间图形．利用它们的侧面展开图，我们可以把这种空间图形的某些问题转化为平面图形得到解决．我们来看下面一个有趣的问题．

　　[例2] 已知圆锥底面直径AB=20，母线SA=30．C为母线SB的中点．今有一小虫沿圆锥侧面从A点爬到C点觅食．问它爬过的最短距离应是多少？

　　分析：小虫沿圆锥侧面从A点爬到C点，其轨迹是空间的一条曲线，且在一曲面上．问题如何解决呢？依题意我们画出圆锥的侧面展开图，如图3所示．不难看出，母线SB把扇形分成相等的两部分．从A点到C点的线段AC的长度就是所求的最短距离．

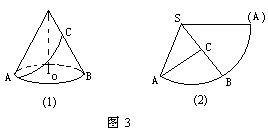
　　把空间问题化归到平面上，巧妙在得到解决。请同学们自己作出解答，看是否能得到正确答案： 。

返回页首