第四节 不等式的解法举例

解无理不等式

　　我们已经学习了一元一次、一元一次不等式（组）、含有绝对值不等式、分式不等式、高次不等式的解法，还有无理不等式的解法，解无理不等式的关键是将它转化为有理不等式来解，以下举例说明。

1．解不等式 .
　　错解：     即   不等式的解集为
错误原因：直接平方去根号，转化为有理不等式，但并不是同解变形，不能保证根式有意义。

　　正确解法：原不等式等价于 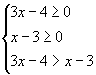  即   

　　故不等式的解集为 .

　　得出一般结论：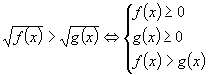

 2．解不等式 .

　　错解：原不等式等价于 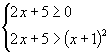   即

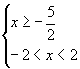
　　 不等式的解集为

　　错误原因：只注意保证根号内被开方式非负，忽略了不等式右边小于零时，不可直接平方，因而不是同解变形。

　　正确解法：原不等式等价于 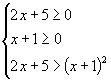  或 .

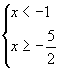
　　即 或   或

　　故原不等式的解集是 .

　　结出一般结论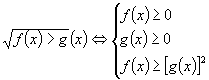： 或

返回顶部