第三节不等式的证明

作者：未知来源：中央电教馆时间：2006/4/8 18:03:15阅读：nyq

字号：小|大

应用三个基本问题证明不等式

江苏东台市城南中学赵庆华王茂森

　　两点之间的距离，线段的定比分点和两点之间的斜率，这三个公式是解析几何中的三个基本问题，凭这三个基本公式，能巧证一些不等式，现举数例如下：

　　例1 已知a、b、c、x均为正数，

　　求证：

　　分析：不等式的两边均和解几中两点之间距离公式相似，不妨构造坐标系，应用距离公式来证.

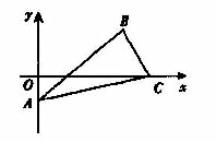　　证明：建立如图所示的坐标系，

　　设连AB、BC、AC，则由两点之间距离公式可得：

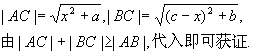
　　当A、C、B三点共线时，即时，不等式取等号.此时，

　　例2 已知

　　证明：当x=0时，结论显然成立.

　　当x＞0时，把看成是x轴上的三点，则分，3所成的比

　　例3 当1＜a＜b时，

　　求证：

　　分析：直接证明有困难，若两边取对数有

　　即

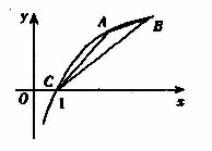
　　联想两点之间的斜率公式，于是可设

　　令C（1，0），A（a,lga）,B(b,lgb)

　　由图象可知，

，

构造函数模型证明不等式

　　有些不等式的证明，如果采用常规方法，往往不易下手或比较冗繁，但若从函数思想考虑，按照函数的某些性质适当构造函数模型，问题可能容易解决.

一、利用单调性构造函数模型证不等式

　　构造一个函数，使原不等式（或经等价变形后）的左右两边是这个函数在某一个单调区间上的两个值，就可以利用函数的单调性证明不等式.

　　例1 已知x＞0,求证：

　　证明：设

　　又

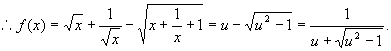
　　当时，这是一个关于的减函数，故当，即

　　例2 已知、、，并且，求证（高中《代数》下册P₁₂例7）

　　证明：考虑函数

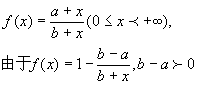
　　所以

　　取

二、利用奇偶性构造函数模型证不等式

　　函数的奇偶性是函数在整个定义域上的性质，由于奇（偶）函数定义域的对称性，故若知道函数在某一区间上的情形，便可知道它在这个区间的对称区间上的情形，这为构造一个函数，运用转化法证明不等式提供了方便和可能.

　　例3 求证

　　证明：考虑函数

　　∴

　　故当

　　说明：不等式两边均含有变量，可考虑“差比较法”.又由于，需对分别判别，故首先考察函数f(x)的奇偶性.

三、利用最值性构造函数模型证不等式

　　对于两个函数

　　例4 已知为实数，试证

　　证明：考虑函数

　　则

　　根据二次函数

时，具有最小值，且

四、构造二次函数模型证不等式

　　二次函数、一元二次方程、二元二次不等式联系极为密切.对于某些条件二次不等式的证明，可以考虑构造相应的二次函数模型，然后利用一元二次方程的根的判别式来转化原问题，从而使原不等式得以证明.

　　例5 已知

　　证明：考虑函数

　　又的系数大于零，

的值恒大于或等于零.

　　例6 已知都是实数，求证：

　　证明：若均为零，则不等式显然成立.

　　若中至少有一个不为零，考虑函数

　　而

　　又二次项系数

　　∴

　　这就是著名的柯西不等式当时的情形.

作者：安徽省和县第二中学何宗祥

累加法证明不等式三例

江苏省昆山震川高级中学王福楠（215300）

　　累加法是证明不等式的一种基本而又重要的方法，在使用这一方法时，如能根据所证不等式取等号的条件，灵活应用平均值不等式，往往能直接推得所需结论.下面我们略举三例，以示说明.

　　例1 设均为正数，且

　　证明：注意到上述不等式当时取等号，由二元均值不等式可得：

三式累加，得

将代入，即得

　例2 设α、β、γ均为锐角，且

　证明：注意到上述不等式当α=β=γ时取等号，由三元均值不等式可得

三式累加，得

=1代入，即得

　　例3 设均为正数，求证

　　证明：注意到上述不等式当时取等号，由四元均值不等式可得

三式累加，得

数学命题的证明方法

　　一个数学命题的证明，按其推理程序的顺逆分为综合法与分析法．由已知到结论顺推者叫综合法，即由因导果的推理方法．由结论到已知逆溯者叫分析法，即执果索因的推理方法．
　　在论证过程中，就其论据的普遍性与特殊性，可分为演绎法与归纳法，即由普遍推知特殊的论证方法称演绎法，反之由特殊归纳出一般的论证方法称归纳法．
　　另外，数学命题的证明，就其所论证的对象是原命题还是等效命题又分为直接证法与间接证法，直接证明原命题者称直接证法．转而证明等效命题者称为间接证法．

用反证法证明不等式

一、反证法的含义

　　反证法是指“证明某个命题时，先假设它的结论的否定成立，然后从这个假设出发，根据命题的条件和已知的真命题，经过推理，得出与已知事实（条件、公理、定义、定理、法则、公式等）相矛盾的结果．这样，就证明了结论的否定不成立，从而间接地肯定了原命题的结论成立．”这种证明的方法，叫做反证法．

二、反证法的严密性

　　数学证明方法可分为直接证法和间接证法，从原命题所给的条件出发，根据已有的公理、定义、法则、公式，通过一系列的推理，一直推到所要证明的命题的结论，这种证法叫做直接证法．有些命题不易用直接证法去证明，这时可通过证明它的等价命题真，从而断定原命题真，这种证法叫做间接证法．数学中常用的间接证法有反证法．

　　既然反证法是间接证法，那么反证法也是通过证明原命题的等价命题从而证明原命题的．

三、反证法证题的步骤

用反证法证题一般分为三个步骤：

　　1、假设命题的结论不成立；

　　2、从这个结论出发，经过推理论证，得出矛盾；

　　3、由矛盾判定假设不正确，从而肯定命题的结论正确．

　　即：提出假设——推出矛盾——肯定结论．

四、反证法的分类

　　反证法中有归谬法和穷举法两种．

　　原命题的结论的否定只有一种情况，只要把这种情况推翻，就可以肯定原命题结论成立，这种反证法叫做归谬法；如果原命题的结论的否定不止一种情况，那么就必须把这几种情况一一否定，才能肯定原命题结论成立，这种反证法叫做穷举法．

五、反证法中常见的矛盾形式

　　（1）与已知条件即题设矛盾；