怎样设计和分析透镜或面镜的实验共轭点

　　我们知道，在方程

　　u和v是对应的，u和v能互换位置。所以，当一个物体放在某个位置上能得到一个实像时，可以把物体移到像的位置，在物体原来所在的位置就会得到一个像。这样可以互换的位置叫做面镜或透镜的“共轭点”。

　　这意味着我们可以在物体距透镜（或面镜）各种距离时测出它和它的像的位置──物距u和像距v，而在以后的对于测量数据的分析（例如制表，或作图）中，每一对观测到的数据都可以再用一次，即把u的值作为v，和把v的值作为u。例如，设透镜的焦距为200mm，物体位于200mm至400mm之间，像就相应地在无限远和400mm之间。在实验中，开始我们把物体放在250mm处，在1000mm处就会产生它的像，此后，每次移动物体30mm直至离透镜400mm；在物距为400mm处，它的像距也是400mm。如果我们把物体继续向外移到更远处，那么所研究的这些点不过是已经试验过的一些点的共轭点。这样继续做下去是浪费时间，因为将得到的那些观测数据可以简便地从我们已取 得的u、v值对调一下就得到了。因此，在通常情况，做这类实像的实验是把物距保持在f至2f范围内，而测量的像距可在一个很长的范围取值（当u值接近f时，v值将很大）。

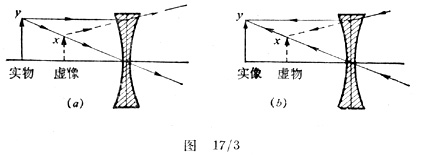
　　在研究虚像时，u和v的值仍可互换，但这时必须改变符号。图17／3（a）表示一个物体和它在x处的虚像。如果光线箭头相反，则我们会得到图17／3（b），在图17／3（b）中朝着x汇集的光线被透镜发散得到一个在y处的实像，光线并非真实地从点x发出，而是认为有一个虚物在x处。根据这点可以认为一个真实物体和它的虚像能“共轭”于一个虚物和其实像。像前面所说的那样，把u，v互换时必须考虑符号。类似的讨论能用于所有的虚像，不管它们是由透镜或面镜会聚而成还是发散而成。考虑到所有可能的情况，可以作出一套完整的图形。建议读者进行这方面的练习。这类练习的全部结果都可以概括到图17／4所示的图象中。可以看出，在第一象限里的点，它们的共轭点也在第一象限内，在第四象限内的点的共轭点则在第二象限内，在第三象限内的点的共轭点也在第三象限内。

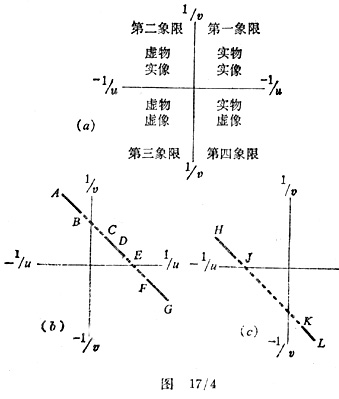
　　在实践中，不借助辅助的透镜或面镜就不能产生虚物。所以，在通常情况下不研究它们，也因而得不到第三象限的点。

　　对于用会聚透镜和会聚面镜所做的实验，将得到沿着图17／4（b）中DE和FG的点，而得不到EF部分的点，因为，与这些点共轭的v值太大了。这条线的其余部分是根据共轭点来绘制的──CD是由ED上的那些点的共轭点组成的，AB是由GF上的各点的共轭点组成的。

　　由于我们不研究虚物，用一个发散透镜或者发散面镜涉及的范围就不可能宽，实际研究到的只有图17／4（c）中的KL部分。但是，KL部分的共轭点为JH部分，所以能画出整个直线。

　　这些直线在轴上的截距是1／f的值，因为，当v＝∞时，1／v＝0，所以1／u＝1／f。同样地，u＝∞时，1／u＝0，也有1／u＝1／f。

　　因此，所画出的直线具有相等的截距。两个截距都要画在图象上，并且应当在坐标纸上标出它们的值，这是设计你的图象时最重要的一步。完成这步最快的方法是把一对相对应的1／u和1／v加在一起。