 设为首页
设为首页
 加入收藏
加入收藏
(一)教材分析
1.知识结构
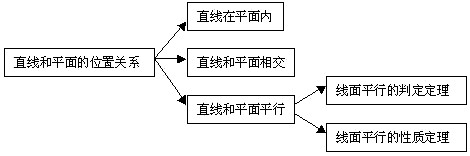
2.重点难点分析
重点:直线与平面平行的判定、性质定理的应用;难点:线面平行的判定定理的反证法证明,线面平行的判定和性质定理的应用.
(1)直线和平面的位置关系
研究直线与平面的位置关系的一般标准:①有无公共点;②直线是否在平面内.可列表如下,见下表:
|
位置关系 |
直线在平面外 |
直线在平面内 |
|
| 直线和平面相交 |
直线和平面平行 |
||
| 定义 |
直线与平面有且只有一个公共点 |
直线和平面没有公共点 |
直线和平面有无数个公共点 |
| 图示 |
|
|
|
| 表示方法 |
|
|
|
|
读法 |
直线
|
直线
|
直线
|
画直线和平面的位置关系示意图要注意:
①线在平面内,直线不要超出表示平面的四边形的各边;
②直线和平面平行,在画图时,平面外的直线要和表示平面的四边形一组对边平行.
(2)直线和平面平行的判定定理
直线和平面平行的判定定理是研究直线与平面、平面与平面位置关系的基础,这个定理是用直线与直线的平行来判定直线与平面平行的,可以简记为“线线平行,则线面平行”,在这里线、线平行的条件是非常重要的,即一条直线在平面外,一条直线在平面内,不注意这个条件,只注意到线、线平行,往往会发生判断错误.
要在理解的基础上记忆直线和平面平行的判定定理,此定理是判定直线平行平面的依据,用符号语言描述为:
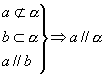 .要注意三个条件必须齐备.
.要注意三个条件必须齐备.
利用直线和平面平行的判定定理证明问题时,一定要说明“平面外的一条直线和平面内的一条直线平行”,若不注明和平面内的直线平行,证明过程不完备.
(3)直线和平面平行的性质定理
直线和平面平行的性质定理的证明要抓住以下两点:其一是由于已知直线与已知平面平行,则这条已知直线和已知平面内的所有直线都没有公共点,其二是过已知直线的平面与已知平面的交线与已知直线在同一平面内.根据以上两点,就可以判定已知直线和交线互相平行了.这个定理可以简记为“若线面平行,则交线平行”.
理解直线与平面平行的性质定理时,要强调条件“经过这条直线的平面与这个平面相交”,防止误解为“一条直线平行于一个平面,就平行于这个平面内的一切直线”.
(二)教法建议
(1)从实际生活入手,多举一些实例,引入直线和平面的位置关系,启发学生自己进行线面位置关系的分类.可以以足球门和地面、教室里墙面的交线与地面等为例.
(2)对于直线与平面平行的判定定理,可从学生的实际经验和直观感觉入手,如:怎样放置跳高的跳高竿,使竿子与地面平行?实际经验启示:只需竿子与地面中的一条线平行,由此揭示直线与平面平行的判定依赖于直线与直线平行.但这两直线必须一条在面内,另一条在面外.
(3)应用直线和平面平行的性质定理,学生较容易用错,教学中不妨采用“找错教学”,学生练习证明时,将出错学生的解法投影出来,让其他的学生寻找错误,这样学生对于它的应用印象要深一些.
(4)注意采用多媒体教学手段,条件允许的学校,可以演示一些多媒体课件,帮助学生理解.