 设为首页
设为首页
 加入收藏
加入收藏
动量守恒定律教学设计方案
一、教学目标
1、知道动量守恒定律的内容,掌握动量守恒定律成立的条件,并在具体问题中判断动量是否守恒.
2、学会沿同一直线相互作用的两个物体的动量守恒定律的推导.
3、知道动量守恒定律是自然界普遍适用的基本规律之一.
二、重点、难点分析
1、重点是动量守恒定律及其守恒条件的判定.
2、难点是动量守恒定律的矢量性.
三、教具
1、气垫导轨、光门和光电计时器,已称量好质量的两个滑块(附有弹簧圈和尼龙拉扣).
2、计算机(程序已输入).
四、教学过程
(一)引入新课
前面已经学习了动量定理,下面再来研究两个发生相互作用的物体所组成的物体系统,在不受外力的情况下,二者发生相互作用前后各自的动量发生什么变化,整个物体系统的动量又将如何?
(二)教学过程设计
以两球发生碰撞为例讨论“引入”中提出的问题,进行理论推导.
画图:
![]()
设想水平桌面上有两个匀速运动的球,它们的质量分别是 ![]() 和
和 ![]() ,速度分别是
,速度分别是 ![]() 和
和 ![]() ,而且
,而且 ![]() .则它们的总动量(动量的矢量和)
.则它们的总动量(动量的矢量和) ![]() .经过一定时间
.经过一定时间 ![]() 追上
追上 ![]() ,并与之发生碰撞,没碰后二者的速度分别为
,并与之发生碰撞,没碰后二者的速度分别为 ![]() 和
和 ![]() ,此时它们的动量的矢量和,即总动量
,此时它们的动量的矢量和,即总动量 ![]()
板书: ![]()
![]()
下面从动量定理和牛顿第三定律出发讨论p和 ![]() 有什么关系.
有什么关系.
设碰撞过程中两球相互作用力分别是 ![]() 和
和 ![]() ,力的作用时间是t.根据动量定理,
,力的作用时间是t.根据动量定理, ![]() 球受到的冲量是
球受到的冲量是 ![]() ;
; ![]() 球受到的冲量是
球受到的冲量是 ![]() .
.
根据牛顿第三定律, ![]() 和
和 ![]() 大小相等,方向相反,即
大小相等,方向相反,即 ![]() .
.
板书: ![]() ①
①
![]() ②
②
![]() ③
③
将①、②两式代入③式应有
板书: ![]()
整理后可得
板书: ![]()
或写成: ![]()
就是: ![]()
这表明两球碰撞前后系统的总动量是相等的.
分析得到上述结论的条件:
1、两球碰撞时除了它们相互间的作用力(这是系统的内力)外,还受到各自的重力和支持力的作用,但它们彼此平衡.桌面与两球间的滚动摩擦可以不计,所以说 ![]() 和
和 ![]() 系统不受外力,或说它们所受的合外力为零.
系统不受外力,或说它们所受的合外力为零.
2、结论:相互作用的物体所组成的系统,如果不受外力作用,或它们所受外力之和为零,则系统的总动量保持不变.这个结论叫做动量守恒定律.
做此结论时引导学生阅读“选修本(第三册)”第110页.并板书:
![]() 时
时 ![]()
3、利用气垫导轨上两滑块相撞过程演示动量守恒的规律.
(1)两滑块弹性对撞(将弹簧圈卡在一个滑块上对撞)
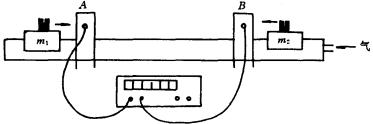
光电门测定滑块 ![]() 和
和 ![]() 第一次(碰撞前)通过A、B光门的时间
第一次(碰撞前)通过A、B光门的时间 ![]() 和
和 ![]() 以及第二次(碰撞后)通过光门的时间
以及第二次(碰撞后)通过光门的时间 ![]() 和
和 ![]() .光电计时器记录下这四个时间.
.光电计时器记录下这四个时间.
将 ![]() 、
、 ![]() 和
和 ![]() 、
、 ![]() 输入计算机,由编好的程序计算出
输入计算机,由编好的程序计算出 ![]() 、
、 ![]() 和
和 ![]() 、
、 ![]() .将已测出的滑块质量
.将已测出的滑块质量 ![]() 和
和 ![]() 输入计算机,进一步计算出碰撞前后的动量
输入计算机,进一步计算出碰撞前后的动量 ![]() 、
、 ![]() 和
和 ![]() 、
、 ![]() 以及前后的总动量p和
以及前后的总动量p和 ![]() .
.
由此演示出动量守恒.
注意:在此演示过程中必须向学生说明动量和动量守恒的矢量性问题.因为 ![]() 和
和 ![]() 以及
以及 ![]() 和
和 ![]() 方向均相反,所以
方向均相反,所以 ![]() 实际上是
实际上是 ![]() ,同理
,同理 ![]() 实际上是
实际上是 ![]() .
.
(2)两滑动完全非弹性碰撞(就弹簧圈取下,两滑块相对面各安装尼龙子母扣)
为简单明了起见,可让滑块 ![]() 静止在两光电门之间不动(
静止在两光电门之间不动( ![]() ),滑块
),滑块 ![]() 通过光门A后与滑块
通过光门A后与滑块 ![]() 相撞,二者粘合在一起后通过光门
B.
相撞,二者粘合在一起后通过光门
B.
光门A测出碰前 ![]() 通过A时的时间t,光门B测出碰后
通过A时的时间t,光门B测出碰后 ![]() 通过B时的时间
通过B时的时间 ![]() .将t和
.将t和 ![]() 输出计算机,计算出
输出计算机,计算出 ![]() 和
和 ![]() 以及碰前的总动量p(
以及碰前的总动量p( ![]() )和碰后的总动量
)和碰后的总动量 ![]() .由此验证在完全非弹性碰撞中动量守恒.
.由此验证在完全非弹性碰撞中动量守恒.
(3)两滑块反弹(将尼龙拉扣换下,两滑块间挤压一弹簧片)
将两滑块置于两光电门中间,二者间挤压一弯成 ![]() 形的弹簧片(铜片).同时松开两手,弹簧片将两滑块弹开分别通过光电门A和B,测定出时间
形的弹簧片(铜片).同时松开两手,弹簧片将两滑块弹开分别通过光电门A和B,测定出时间 ![]() 和
和 ![]() .
.
将 ![]() 和
和 ![]() 输入计算机,计算出
输入计算机,计算出 ![]() 和
和 ![]() 以及
以及 ![]() 和
和 ![]() .
.
引导学生认识到弹开前系统的总动量 ![]() ,弹开后系统的总动量
,弹开后系统的总动量 ![]() .
.
总动量守恒,其数值为零.
4、例题:甲、乙两物体沿同一直线相向运动,甲的速度是3m/s,乙物体的速度是1m/s.碰撞后甲、乙两物体都沿各自原方向的反方向运动,速度的大小都是2m/s.求甲、乙两物体的质量之比是多少?
引导学生分析:对甲、乙两物体组成的系统来说,由于其不受外力,所以系统的动量守恒,即碰撞前后的总动量大小、方向均一样.
由于动量是矢量,具有方向性,在讨论动量守恒时必须注意到其方向性.为此首先规定一个正方向,然后在此基础上进行研究.
板书解题过程,井边讲边写.
板书:
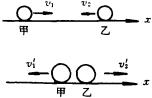
讲解:规定甲物体初速度方向为正方向.则 ![]() m/s,
m/s, ![]() m/s.碰后
m/s.碰后 ![]()
根据动量守恒定律应有: ![]()
移项整理后可得 ![]() 比
比 ![]() 为
为 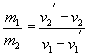
代入数值后可得 ![]()
即甲、乙两物体的质量比为3:5.
5、练习题
质量为30kg的小孩以8m/s的水平速度跳上一辆静止在水平轨道上的平板车,已知平板车的质量是80kg,求小孩跳上车后他们共同的速度.
分析:对于小孩和平板车系统,由于车轮和轨道间的滚动摩擦很小,可以不予考虑,所以可以认为系统不受外力,即对人、车系统动量守恒.
板书解题过程:
跳上车前系统的总动量 ![]()
跳上车后系统的总动量 ![]()
由动量守恒定律有度
![]()
解得: ![]()
6、小结
(1)动量守恒的条件:系统不受外力或合外力为零时系统的动量守恒.
(2)动量守恒定律适用的范围:适用于两个或两个以上物体组成的系统.动量守恒定律是自然界普遍适用的基本规律,对高速或低速运动的物体系统,对宏观或微观系统它都是适用的.
动量守恒定律的教学设计方案
通过演示实验及推导,使学生掌握动量守恒的条件及适用范围.
课时安排:1课时
教学用具:演示动量守恒的小车、弹簧和长玻璃板、砝码等(或验证动量守恒定律的气垫导轨和滑块、充气机等).
师生互动活动设计:
1、教师做好演示实验,从理论上推导动量守恒定律.
2、学生观察、分析演示实验.
教学过程:
一、引入新课
问题提出:两个相互作用的物体,在没有外力作用下,它们的动量变化服从什么规律?
演示实验:如图所示,在光滑水平面MN上放两等质量的小车A、B,小车间夹一个弹簧,使弹簧处于压缩状态,并用线拴住小车.用火柴烧断线,由于弹簧的弹力,两车分离,并沿着相反方向运动,同时撞到等距离的挡板C、D上,这说明它们碰撞后总动量即动量的矢量和为零,也就是说,它们碰撞前后动量守恒.
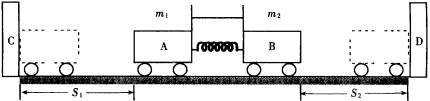
二、理论推导
如果使两小车的质量之比 ![]() ,重复上面的实验,可以近似地得到
,重复上面的实验,可以近似地得到 ![]() 关系,这说明它们碰撞前后动量守恒.
关系,这说明它们碰撞前后动量守恒.
理论推导:
设在光滑水平面上做匀速运动的两个小球,质量分别是 ![]() 和
和 ![]() ,沿着同一直线向相同的方向运动,速度分别是
,沿着同一直线向相同的方向运动,速度分别是 ![]() 和
和 ![]() ,且
,且 ![]() 两个小球的总动量为:
两个小球的总动量为:
![]()
经过一段时间后,两个发生碰撞,碰撞后的速度分别是 ![]() 和
和 ![]() ,碰撞后的总动量为:
,碰撞后的总动量为:
![]()
设碰撞过程中第一个球和第二个球所受的平均作用力分别是 ![]() 和
和 ![]() ,力的作用时间是t.根据动量定理,第一个球受到的冲量是:
,力的作用时间是t.根据动量定理,第一个球受到的冲量是:
![]() ,
,
第二个球受到的冲量是:
![]() .
.
根据牛顿第三定律, ![]() 和
和 ![]() 大小相等,方向相反.所以:
大小相等,方向相反.所以:
![]()
由此得 ![]()
或者 ![]()
![]()
上式表明碰撞前后的总动量相等.
教师提出问题让学生们思考:动量守恒的条件是什么呢?
介绍基本概念:系统、内力、外力后得出动量守恒的条件.
一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变.
(一)写出动量守恒定律数学表达式的几种形式:
1、 ![]()
2、 ![]()
强调动量守恒定律的表达式是矢量式,速度v必须对同一参考系,通常取地面为参考系.
举例说明动量守恒定律的适用条件,即“一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变.”这是所说的“外力之和”与“合外力”不是一个概念.“合外力”是指作用在某个物体(质点)上的外力的矢量和,而“外力之和”是指把作用在系统上的所有外力平移到某点后算出矢量和.
(二)推广动量守恒的适用条件:
1、系统外力之和不为零,但系统相互作用力远大于外力,但相互作用时间极短,也可认为动量守恒,如碰撞、爆炸等.
2、系统外力之和不为零,但某一方向外力之和为零,系统在该方向动量守恒.
(三)说明动量守恒定律的适用范围
3、既适用正碰,也适用于斜碰,不仅适用于碰撞,也适用于各种相互作用.
4、不仅适用于两个物体组成的系统,也适用于多个物体组成的系统.
5、不仅适用于低速宏观物体,也适用于高速微观系统.
三、思考与讨论:
在图中所示的装置中,木块B与水平桌面间的接触是光滑的,子弹A沿水平方向射入木块后,留在木块内,将弹簧压缩到最短.现将子弹、木块和弹簧(质量不可以忽略)合在一起作为研究对象(系统),此系统从子弹开始射入木块到弹簧压缩至最短的整个过程中,动量是否守恒?说明理由.
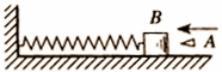
分两个过程讨论:将子弹、木块和弹簧(质量不可忽略)合在一起作为一个研究对象(系统),子弹射入木块时间极短,弹簧未压缩,系统动量守恒,设子弹质量为m,初速为 ![]() ,木块质量为M,射入后子弹和木块立刻有相同的末速度v.对系统进行受力分析,得出系统在这一极短时间在水平方向不受外力,竖直方向外力之和为零,系统动量守恒.
,木块质量为M,射入后子弹和木块立刻有相同的末速度v.对系统进行受力分析,得出系统在这一极短时间在水平方向不受外力,竖直方向外力之和为零,系统动量守恒.
有 ![]()
![]()
子弹和木块以共同速度v推动弹簧向左运动,弹簧发生形变,此过程系统水平方向受到墙壁向右的作用力,系统动量不守恒.
五、例题讲解
【例】平板小车C放在光滑的水平地面上,车上表面粗糙,车上有A、B两个木块,中间有一轻细弹簧,弹簧压缩, ![]() ,突然释放弹簧,则(CD)
,突然释放弹簧,则(CD)
A.若A、B与平板车上表面的动摩擦因数相同,A、B、C系统动量守恒.
B.若A、B与平板车上表面的动摩擦因数不相同,A、B、C组成的系统动量不守恒.
C.若A、B所受摩擦力大小相等,A、B组成的系统动量守恒.
D.若A、B所受摩擦力大小不相等,A、B、C组成的系统动量仍守恒.引导学生分析系统的受力情况,区别内力与外力,从而选择正确答案.
六、总结、扩展
1、动量定理适用于单个物体,动量守恒定律适用于系统.
2、动量守恒定律的同一性和瞬时性.
同一性:速度v必须对同一参考系,通常取地面为参考系.
瞬时性: ![]() 是系统相互作用初始时刻的总动量.
是系统相互作用初始时刻的总动量.
![]() 是系统相互作用末了时刻的总动量.
是系统相互作用末了时刻的总动量.
3、判断动量守恒,必须明确研究对象—系统,从而确定哪些力是内力,哪些力是外力.
七、板书设计
动量守恒定律
一、基本概念
l、系统:
2、内力:
3、外力:
二、动量守恒定律
1、内容
2、表达式 ![]()
3、适用条件
4、适用范围