 设为首页
设为首页
 加入收藏
加入收藏
关于伯努利方程的教学设计
一、教学目标
1、知道什么是理想流体,知道什么是流体的定常流动。
2、知道伯努利方程,知道它是怎样推导出来的,会用它解释一些现象。
3、通过在流体力学中应用功和能的关系推导伯努利方程,培养学生使用能量守恒思想
的意识和思路。
4、通过对实例的定性分析,培养学生对实际问题的建立模型和分析推力能力,学以致用。并在使用中体会物理规律在实际生活中的意义。
二、教学建议
1、教材分析:本节内容从建立流体的理想模型——理想流体开始,简单介绍了流体的特点及流体的定常流动方式。重点依据功能关系推导了理想流体作定常流动时,流体中压强和流速的规律——伯努利方程。并使用伯努利方程对大量生活实例进行了定性分析。
2、教法建议:本节主要是初步介绍了流体动力学的点滴知识,且作为选学内容,主要是开阔视野,培养知识、方法迁移能力,为学有余力的同学自我加深准备的。所以在教学中要以基本概念建立、基本思路迁移、基本分析方法使用为重点,不要在知识深度上过于下功夫。建议在学生有引导的自学的基础之上,讨论归纳,以便突出上述重点,遗留问题,供有兴趣的学生进一步学习。
三、教学设计示例
教学重点:如何利用功能关系推导伯努利方程;如何利用该方程解释实际问题。
教学难点:如何利用功能关系推导伯努利方程;如何利用该方程解释实际问题。
示例:
(一)课前预习提纲
1、流体主要有哪些特点?什么是理想流体?
2、什么是定常流动?什么是流线?如何用流线形象的表示流体的流动?
3、仔细阅读书P152伯努利方程的推导过程,并思考下列问题:(1)伯努利方程表述的是什么规律? (2)对于推导过程中所选取的研究对象,是谁对它作了功,为什么?研究对象的机械能如何变化了,为什么?能否口述之。(3)你认为推导过程中最重要的是什么?难点是什么?
4、自己做书P151的小实验,认真阅读书P154的应用举例,归纳思路,并试做书P155的练习七。
(二)课上
带领学生通过讨论预习提纲建立概念、思路,解决疑难。要让学生充分发言。
预习题简答:(仅供参考)
1、答:实际流体具有可压缩性和粘滞性。但因一般液体的可压缩量很小,可以不予考虑;而气体的压缩性虽然较强,但若流动的气体中各处的密度不随时间发生明显的变化时,也可以不考虑其压缩性。另外,在某些问题中,若流体的流动形式主要的,而粘滞性是次要的,则可认为该流体没有粘滞性。不可压缩的、没有粘滞性的流体就是理想流体。理想流体实际上是一个理想的物理模型。
2、答:流体质点经过空间各点的流速虽然可以不同,但如果空间每一点的流速不随时间而改变,这样的流动方式称为定常流动,也可称为稳定流动。这也是一种理想化的流动方式。
在定常流动的流体中,假象沿着各液体质点的运动轨迹画出许多曲线,这些线就叫做流线。流线在某一点的切线方向表示该点的流速方向,流线的疏密表示流速的大小,即流线越密,表示流速越大。
3、答:(1)伯努利方程表述的是理想流体作定常流动时,流体中压强和流速的规律。
其规律为: ![]() 常量。
常量。
(2)因为理想流体没有粘滞性,不能被压缩,所以b1a2位置流体的机械能没有变化,整个流体的机械能变化可等效为a1b1位置流体迁移到a2b2位置的过程中机械能的变化。依据功能关系,这样的机械能变化等于研究对象在a1和a2两个截面上所受外力做功之和。
(3)略。
4、 略。
参考答案:略。
关于伯努利方程的知识讲解
把一个乒乓球放在倒置的漏斗中间(图8-29),向漏斗口吹气,会把乒乓球吹跑吗?实际正好相反,乒乓球会贴在漏斗上不掉下来.平行地竖放两张纸,向它们中间吹气,会把两张纸吹开吗?实际正好相反,两张纸会贴近(图8-30).

怎样解释上述现象呢?现象中涉及空气的流动.你可能不会想到,解释上述现象,跟说明飞机能够上天,用的是同一个道理,这就是流动的流体中压强和流速的关系.通常把液体和气体统称流体。
这一节把功能关系应用到流动的流体中,推导压强和流速的关系.研究流体的流动,是一门复杂的学问.初步进行研究,需要作一些限定,采用简单的物理模型,这就是理想流体的定常流动.
理想流体 液体不容易被压缩,在不十分精确的研究中可以认为液体是不可压缩的.气体容易被压缩,但在研究流动的气体时,如果气体的密度没有发生显著的改变,也可以认为气体是不可压缩的.
流体流动时,速度不同的各层流体之间有摩擦力,也就是说,流体具有粘滞性.不同的流体,粘滞性不同.油类的粘滞性较大,水、酒精的粘滞性较小,气体的粘滞性更小.研究粘滞性小的流体,在有些情况下可以认为流体没有粘滞性.
不可压缩的、没有粘滞性的流体,称为理想流体.
定常流动 观察一段河床比较平缓的河水的流动,你可以看到河水平静地流着,过一会儿再看,河水还是那样平静地流着,各处的流速没有什么变化.河水不断地流走,可是这段河水的流动状态没有改变.河水的这种流动就是定常流动.流体质点经过空间各点的流速虽然可以不同,但如果空间每一点的流速不随时间而改变,这样的流动就叫做定常流动.自来水管中的水流,石油管道中石油的流动,都可以看作定常流动.

流体的流动可以用流线形象地表示.在定常流动中,流线表示流体质点的运动轨迹.图8-31是液体流过圆柱体时流线的分布.AB处液体流过的横截面积大,CD处液体流过的横截面积小,液体在CD处流得急,流速大.AB处的流线疏,CD处的流线密.这样,从流线的分布可以知道流速的大小.流线疏的地方,流速小;流线密的地方,流速大.
伯努利方程 现在研究理想流体做定常流动时,流体中压强和流速的关系.
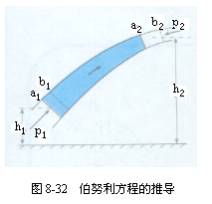
图8-32表示一个细管,其中流体由左向右流动.在管的a1处和a2处用横截面截出一段流体,即a1处和a2处之间的流体,作为研究对象.
a1处的横截面积为S1,流速为v1,高度为h1.a1处左边的流体对研究对象的压强为p1,方向垂直于S1向右.
a2处的横截面积为S2,流速为v2,高度为h2.a2处右边的流体对研究对象的压强为p2,方向垂直于S2向左.
经过很短的时间间隔Δt,这段流体的左端S1由a1移到b1,右端S2由a2移到b2.两端移动的距离分别为Δl1和Δl2.左端流入的流体体积为ΔV1=S1Δl1,右端流出的流体体积为ΔV2=S2Δl2,理想流体是不可压缩的,流入和流出的体积相等,ΔV1=ΔV2,记为ΔV.
现在考虑左右两端的力对这段流体所做的功.作用在左端的力F1=p1S1,所做的功W1=F1Δl1=p1S1Δl1=p1ΔV.作用在右端的力F2=p2S2,所做的功
W2=-F2Δl2=-p2S2Δl2=-p2ΔV.外力所做的总功
W=W1+W2=(p1-p2)ΔV. (1)
外力做功使这段流体的机械能发生改变.初状态的机械能是a1到a2这段流体的机械能E1,末状态的机械能是b1到b2这段流体的机械能E2.由b1到a2这一段,经过时间Δt,虽然流体有所更换,但由于我们研究的是理想流体的定常流动,流体的密度ρ和各点的流速v没有改变,动能和重力势能都没有改变,所以这一段的机械能没有改变.这样,机械能的改变E2-E1就等于流出的那部分流体的机械能减去流入的那部分流体的机械能.
![]()
![]()
力势能为mgh2=ρgh2ΔV.机械能的改变为
![]()
右边对这段液体的的作用力向左,而这段液体的位移向右,所以功是负值。
理想流体没有粘滞性,流体在流动中机械能不会转化为内能,所以这段流体两端受的力所做的总功W等于机械能的改变E2-E1,即
W=E2-E1 (3)
将(1)式和(2)式代入(3)式,得
![]()
整理后得
![]()
a1和a2是在流体中任意取的,所以上式可表达为:对管中流体的任意处,
![]()
(4)式和(5)式称为伯努利方程.
流体水平流动时,或者高度差的影响不显著时(如气体的流动),伯努利方程可表达为
![]()

从(6)式可知,在流动的流体中,压强跟流速有关,流速v大的地方压强p小,流速v小的地方压强p大.知道压强和流速的关系,就可以解释本节开始所做的实验了.经过漏斗吹乒乓球时,乒乓球上方空气的流速大,压强小,下方空气的压强大,乒乓球受到向上的力,所以会贴在漏斗上不掉下来.向两张纸中间吹气时,两张纸中间空气的流速大,压强小,外边空气的压强大,所以两张纸会贴近.同样的道理,两艘并排的船同向行驶时(图8-33),如果速度较大,两船会互相靠近,有相撞的危险.历史上就曾经发生过这类事故.在航海中,对并排同向行驶的船舶,要限制航速和两船的距离.
应用举例 飞机为什么能够飞上天?因为机翼受到向上的升力.图8-34甲表示飞机飞行时机翼周围空气的流线分布.机翼横截面的形状上下不对称,机翼上方的流线密,流速大,下方的流线疏,流速小.由伯努利方程可知,机翼上方的压强小,下方的压强大.这样就产生了作用在机翼上的向上的升力.
根据运动的相对性,可以认为船静止,水流动.

喷雾器(图8-35)是利用流速大、压强小的原理制成的.让空气从小孔迅速流出,小孔附近的压强小,容器里液面上方的空气压强大,液体就沿小孔下边的细管升上来,从细管的上口流出后,受气流的冲击,被喷成雾状.
汽化器俗称化油器
汽油发动机的汽化器,与喷雾器的原理相同.汽化器是向气缸里供给燃料与空气的混合物的装置,构造原理如图8-36所示.当气缸里的活塞做吸气冲程时,南气被吸入管内,在流经管的狭窄部分时流速大,压强小,汽油就从安装在狭窄部分的喷嘴流出,被喷成雾状,形成油气混合物,进入气缸.
球类比赛中的“旋转球”具有很大的威力.旋转球和不转球的飞行轨迹不同,是因为球周围空气流动情况不同造成的.图8-37甲表示不转球水平向左运动时周围空气的流线.球的上方和下方流线对称,流速相同,上下不产生压强差.现在考虑球的旋转,转动轴通过球心且垂直于纸面,球逆时针旋转.球旋转时会带动周围的空气跟着它一起旋转,致使球的下方空气的流速增大,上方的流速减小,周围空气的流线如图 8-37乙所示.球的下方流速大,压强小,上方流速小,压强大.跟不转球相比,图8-37乙所示的旋转球因为旋转而受到向下的力,飞行轨迹要向下弯曲.
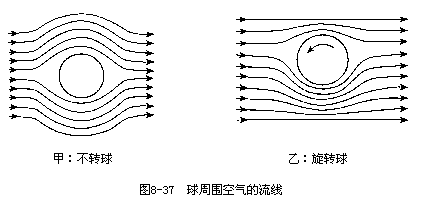
图8-38表示乒乓球的上旋球,转动轴垂直于球飞行的方向且与台面平行,球向图示方向旋转.图8-37乙表示的就是上旋球周围空气的流线.在相同的条件下,上旋球比不转球的飞行弧线要低.下旋球正好相反,球向图示反方向旋转,受到向上的力,比不转球的飞行弧线要高.

物理和体育相通,各项体育运动中都要用到物理知识.