 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例(一)
弧度制
教学目标:
1.明确引入弧度制的必要性,理解新单位制意义.
2.熟练掌握角度制与弧度制的换算.
教学重点:理解弧度制引入的必要性,掌握定义,能熟练地进行角度制与弧度制的互化.
教学难点:弧度制定义的理解.
教学用具:投影仪.
教学过程
1.设置情境
在角度制下,当把两个带着度、分、秒各单位的角相加、相减时,由于运算进率非十进制,总给我们带来不少困难.那么我们能否重新选择角单位,使在该单位制下两角的加、减运算与常规的十进制加减法一样去做呢?本节课就来尝试选择这种新单位.
2.探索研究
(1)复习角度制
我们在平面几何中研究角的度量,当时是用度做单位来度量角, ![]() 的角是如何定义的?
的角是如何定义的?
规定把周角的 ![]() 作为1度的角.
作为1度的角.
我们把用度做单位来度量角的制度叫做角度制,在数学和其他许多科学研究中还要经常用到另一种度量角的制度—弧度制,它是如何定义呢?
(2)弧度制定义
我们把等于半径长的圆弧所对的圆心角叫做1弧度的角,如图1,弧 ![]() 的长等于半径
的长等于半径 ![]() ,
, ![]() 所对的圆心角
所对的圆心角 ![]() 就是1弧度的角,弧度制的单位符号是
就是1弧度的角,弧度制的单位符号是 ![]() ,读作弧度.
,读作弧度.
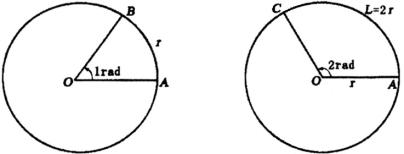
图1
![]() 的弧度数
的弧度数 ![]()
![]() 的弧度数
的弧度数 ![]()
提问:若弧是一个半圆,则其圆心角的弧度数是多少?若弧是一个整圆呢?
因为半圆的弧长 ![]() ,其圆心角的弧度数是
,其圆心角的弧度数是 ![]() ,同理,若弧是一个整圆,其圆心角的弧度数是
,同理,若弧是一个整圆,其圆心角的弧度数是 ![]() .
.
在 ![]() 到
到 ![]() 的角的弧度数
的角的弧度数 ![]() 必然适合不等式
必然适合不等式 ![]() ,角的概念推广后,弧的概念也随之推广,任一正角的弧度数都是一个正数.如果圆心角表示一个负角,且它以所对的弧长
,角的概念推广后,弧的概念也随之推广,任一正角的弧度数都是一个正数.如果圆心角表示一个负角,且它以所对的弧长 ![]() ,则这个圆心角的弧度数是
,则这个圆心角的弧度数是 ![]() ,由此我们给出弧度制的定义:一般地,可以得到:正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0;角
,由此我们给出弧度制的定义:一般地,可以得到:正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0;角 ![]() 的弧度数的绝对值
的弧度数的绝对值 ![]() ,其中
,其中 ![]() 是以角
是以角 ![]() 作为圆心角时所对的弧长,
作为圆心角时所对的弧长, ![]() 是圆的半径,这种以弧度作为单位来度量角的单位制,叫做弧度制.
是圆的半径,这种以弧度作为单位来度量角的单位制,叫做弧度制.
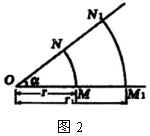 提问:为什么可以用弧长与其半径的比值来度量角的大小呢?即这个比值是否与所取的圆的半径大小无关呢?
提问:为什么可以用弧长与其半径的比值来度量角的大小呢?即这个比值是否与所取的圆的半径大小无关呢?
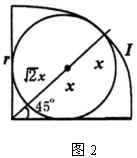
如图2,设 ![]() 为
为 ![]() 的角,圆弧
的角,圆弧 ![]() 和
和 ![]() 的长分别为
的长分别为 ![]() 和
和 ![]() ,点
,点 ![]() 和
和 ![]() 到点
到点 ![]() 的距离(即圆半径)分别为
的距离(即圆半径)分别为 ![]()
![]() 和
和 ![]()
![]() ,由初中学过的弧长公式可得:
,由初中学过的弧长公式可得: ![]() ,
, ![]() ,于是
,于是 ![]() .上式表明,以角
.上式表明,以角 ![]() 为圆心角所对的弧长与其半径的比值,由
为圆心角所对的弧长与其半径的比值,由 ![]() 的大小来确定,与所取的半径大小无关,仅与角的大小有关.
的大小来确定,与所取的半径大小无关,仅与角的大小有关.
因 ![]() ,可以得到
,可以得到 ![]() ,那弧长等于圆弧所对圆心角的弧度数的绝对值与半径的积,这个公式比采用角度制时相应公式
,那弧长等于圆弧所对圆心角的弧度数的绝对值与半径的积,这个公式比采用角度制时相应公式 ![]() 要简单.
要简单.
(3)角度制与弧度制的换算
用“弧度”与“度”去度量每一个角时,除了零角以外,所得到的量数都是不同的,但它们既然是度量同一个角的结果,二者就可以相互换算.我们已经知识若弧是一个整圆,它的圆心角是周角,其弧度数是 ![]() ,而在角度制里它是
,而在角度制里它是 ![]() ,因此
,因此 ![]() ,两边除以2.
,两边除以2.
得 ![]() 等式两边同除180
等式两边同除180
得 ![]()
同理,把弧度换成角度.
![]()
![]()
![]()
【例1】把 ![]() 化成弧度.
化成弧度.
解:∵ ![]()
∴ ![]()
【例2】把 ![]() 化成度.
化成度.
解: ![]()
同学们在进行角度制与弧度制互化时要抓住 ![]() 弧度这个关键.
弧度这个关键.
下面请大家写出一些特殊角的弧度数.
| 角度 |
|
|
|
|
|
|
|||||
| 弧度 |
|
|
|
|
|
按从左至右顺序其答案是:0、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() .今后我们用弧度制表示角的时候,“弧度”二字或“
.今后我们用弧度制表示角的时候,“弧度”二字或“ ![]() ”通常省略不写,而只写相应的弧度数.例如:角
”通常省略不写,而只写相应的弧度数.例如:角 ![]() 就表示
就表示 ![]() 是
是 ![]() 的角,
的角, ![]() 就表示
就表示 ![]() 的角的余弦,即
的角的余弦,即 ![]() .
.
(4)角度制与弧度制的比较
引进弧度制后,我们应将它与角度制进行比较,同学们应明确:①弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度;②1弧度是等于半径长的圆弧所对的圆心角(或该弧)的大小,而 ![]() 是圆的
是圆的 ![]() 所对的圆心角(或该弧)的大小;③不论是以“弧度”还是以“度”为单位的角的大小都是一个与半径大小无关的定值.
所对的圆心角(或该弧)的大小;③不论是以“弧度”还是以“度”为单位的角的大小都是一个与半径大小无关的定值.
【例3】计算:
(1) ![]() ;(2)
;(2) ![]() .
.
解:(1)∵ ![]() ∴
∴ ![]()
(2)∵ ![]()
![]()
练习(用投影仪)
1.把下列各角化成 ![]() 的形式:
的形式: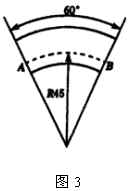
(1) ![]() ;(2)
;(2) ![]() ;
;
(3) ![]() .
.
2.求右图3中公路弯道处弧 ![]() 的长
的长 ![]() (精确到
(精确到 ![]() ,图中长度单位:
,图中长度单位: ![]() ).
).
参考答案:
1.(1) ![]()
(2) ![]()
(3) ![]()
2.∵ ![]()
∴ ![]()
![]()
答:弯道处 ![]() 的长约为
的长约为 ![]() .
.
3.练习反馈
(1)若三角形的三个内角之比是2:3:4,求其三个内角的弧度数.
(2)已知扇形的周长为 ![]() ,面积为
,面积为 ![]() ,求扇形的中心角的弧度数.
,求扇形的中心角的弧度数.
(3)下列终边相同的是( ).
A. ![]() 与
与 ![]()
B. ![]() 与
与 ![]()
C. ![]() 与
与 ![]()
D. ![]() 与
与 ![]()
参考答案:(1) ![]() 、
、 ![]() 、
、 ![]() ; (2)2 (3)B
; (2)2 (3)B
4.总结提炼
(1) ![]() 弧度;
弧度;
(2)“角化弧”时,将 ![]() 乘以
乘以 ![]() ;“弧化角”时,将
;“弧化角”时,将 ![]() 乘以
乘以 ![]()
(3)弧长公式: ![]()
扇形面积公式: ![]() .(其中
.(其中 ![]() 为圆心角
为圆心角 ![]() 所对的弧长,
所对的弧长, ![]() 为圆心角的弧度数,
为圆心角的弧度数, ![]() 为圆半径.)
为圆半径.)
课时作业
1.角集合 ![]() 与
与 ![]() 之间的关系为( )
之间的关系为( )
A.![]() B.
B. ![]() C.
C. ![]() D.不确定
D.不确定
2.若角 ![]() 和
和 ![]() 的终边互为反向延长线,则有( )
的终边互为反向延长线,则有( )
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
3.中心角为 ![]() 的扇形,它的弧长为
的扇形,它的弧长为 ![]() ,则该扇形所在圆的半径为______________.
,则该扇形所在圆的半径为______________.
4.若 ![]() ,且
,且 ![]() 与
与 ![]() 的角的终边垂直,则
的角的终边垂直,则 ![]() .
.
5.已知直径为 ![]() 的滑轮上有一条长为
的滑轮上有一条长为 ![]() 的弦,
的弦, ![]() 是此弦的中点,若滑轮以每秒5弧度的角速度旋转,则经过5秒钟后点
是此弦的中点,若滑轮以每秒5弧度的角速度旋转,则经过5秒钟后点 ![]() 转过的弧长等于多少?
转过的弧长等于多少?
6.已知一个扇形周长为 ![]() ,当扇形的中心角为多大时,它有最大面积
,当扇形的中心角为多大时,它有最大面积
参考答案:1.C 2.D 3.6; 4. ![]() 或
或 ![]() ; 5.
; 5. ![]() ; 6.中心角
; 6.中心角 ![]() 时,
时, ![]() .
.
教学设计示例(二)
弧度制
教学目标
1.理解角集与实数集 ![]() 的一一对应,熟练掌握角度制与弧度制间的互相转化.
的一一对应,熟练掌握角度制与弧度制间的互相转化.
2.能灵活应用弧长公式、扇形面积公式解决问题.
教学重点:能熟练地进行角度制与弧度制的互化.
教学难点:能灵活应用弧长公式、扇形面积公式解决问题.
教学用具:投影仪
教学过程:
1.设置情境.
像角的概念推广一样,我们已经把 ![]() ~
~ ![]() 中角,利用“乘以
中角,利用“乘以 ![]() ”这一法则映射到实数集
”这一法则映射到实数集 ![]() 上,那么,
上,那么, ![]() ~
~ ![]() 以外的角能否化为弧度制?如果能,如何转化呢?乘数因子是否仍为“
以外的角能否化为弧度制?如果能,如何转化呢?乘数因子是否仍为“ ![]() ”,本节课就来讨论这个问题.
”,本节课就来讨论这个问题.
2.探索研究
(1)正、负角的弧度定义.
 正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,角
正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,角 ![]() 的弧度数的绝对值
的弧度数的绝对值 ![]() ,
, ![]() 为以角
为以角 ![]() 作为圆心角的所对的弧的长,
作为圆心角的所对的弧的长, ![]() 是圆的半径,这种以弧度作为单位来度量角的单位制,叫做弧度制.
是圆的半径,这种以弧度作为单位来度量角的单位制,叫做弧度制.
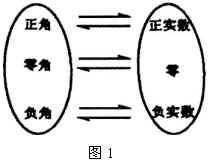
(2)角集合与实数集 ![]() 之间的一一对应
之间的一一对应
用弧度制来度量角,实际上是在角的集合与实数集 ![]() 之间建立这样的一一对应关系(如图1所示).
之间建立这样的一一对应关系(如图1所示).
每一个角都有惟一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有惟一的一个角(角的弧度数等于这个实数)与它对应.
于是,就可以把三角函数看成是以实数为自变量的函数,它的自变量的意义可以有多种解释,从而使三角函数的应用更加广泛,在数学与科学研究中所以普遍采用弧度制,这是原因之一.
(3)有关公式
①弧长 ![]()
② ![]()
(4)例题分析
【例1】下列站个角中哪几个是第二象限角?
(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
(4)9 (5)-4 (6) ![]()
解:(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6)![]()
从而可知(2)(4)(5)所给的角在Ⅱ象限.
点评:①用弧度制表示终边相同的角的方法 ![]()
②把一角化为 ![]() 形式,其中
形式,其中 ![]() 从而可判断角所在象限.
从而可判断角所在象限.
③在同一问题求解过程中,两种单位不能混用,如 ![]() 写法不妥.
写法不妥.
【例2】(1)把 ![]() 化为
化为 ![]() ,
, ![]() ,
, ![]() 的形式是( )
的形式是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(2)在半径不等的两个圆内,1弧度的圆心角( )
A.所对弧长相等 B.所对的弦长相等
C.所对弧长等于各自半径 D.所对的弧长为
![]()
解:∵ ![]()
∴ ![]()
![]()
∴选D.
(2)由弧度制定义,知半径为 ![]() 的圆上,1弧度的弧长应等于半径
的圆上,1弧度的弧长应等于半径 ![]() ,故选
,故选 ![]() .
.
【例3】填空
(1)在 ![]() 内找出与
内找出与 ![]() 终边相同的角______________.
终边相同的角______________.
(2)圆的弧长等于该圆内接正三角形的边长,则该弧所对的圆心角的弧度数是________________.
(3)在扇形 ![]() 中,
中, ![]() ,弧长为1,则此扇形内切圆的面积____________.
,弧长为1,则此扇形内切圆的面积____________.
解:(1)与 ![]() 终边相同角,设为
终边相同角,设为 ![]() .令
.令 ![]()
∴所求角为: ![]() .
.
 (2)设圆半径为
(2)设圆半径为 ![]() ,则内接正三角形边长为
,则内接正三角形边长为 ![]() ,当弧长
,当弧长 ![]() 时,其所对圆心角
时,其所对圆心角 ![]() .
.
(3)如图2,设扇形半径为
![]() ,内切圆半径为
,内切圆半径为 ![]() ,则由
,则由 ![]()
∵ ![]()
∴ ![]()
3.练习反馈
(1) ![]() =___________弧度;
=___________弧度; ![]() =____________弧度;-10弧度_________度
=____________弧度;-10弧度_________度
(2)与 ![]() 终边相同的角是__________,它们是第__________象限角,其中最小正角为__________,最大负角为___________.
终边相同的角是__________,它们是第__________象限角,其中最小正角为__________,最大负角为___________.
参考答案:
(1) ![]() ;
; ![]() ;
; ![]()
(2) ![]() ;它们是第三象限角;最小正角为
;它们是第三象限角;最小正角为 ![]() ,最大负角为
,最大负角为 ![]() .
.
4.总结提炼
(1) ![]() (度)
(度) ![]() ;
; ![]()
这里, ![]() 为任一角度制角,
为任一角度制角, ![]() 为任一实数(弧度)
为任一实数(弧度)
(2)有了弧度制,实现了角度集与实数集合之间的一一对应,对应法则是正比例函数 ![]() .(
.( ![]() 为角度集合中元素,
为角度集合中元素, ![]() 为实数集中元素).
为实数集中元素).
(3)弧度制的引入,使得有关公式表达式简单,运算为常规的十进制.
(4)任一角 ![]() 的弧度的绝对值为
的弧度的绝对值为 ![]() ,也就是说,对于任意角的度量,其弧度要把符号和绝对值分开求.
,也就是说,对于任意角的度量,其弧度要把符号和绝对值分开求.
课时作业
1.若 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() 的终边位置关系是( )
的终边位置关系是( )
A.重合 B.关于原点对称 C.关于 ![]() 轴对称 D.关于
轴对称 D.关于 ![]() 轴对称
轴对称
2.如果弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
3.地球赤道的半径是6370㎞,所以赤道上 ![]() 的弧长是_________(精确到0.01㎞)
的弧长是_________(精确到0.01㎞)
4.一条铁路在转弯处成圆弧形,圆弧的半径为2㎞,一列火车用每小时30㎞的速度通过,10秒间转过几度?
5.半径为 ![]() 的扇形,其周长为
的扇形,其周长为 ![]() ,则扇形中所含弓形的面积是多少?
,则扇形中所含弓形的面积是多少?
6.角 ![]() 和角
和角 ![]() 的和是1弧度,差为
的和是1弧度,差为 ![]() ,则
,则 ![]() 和
和 ![]() 的弧度数分别是多少?
的弧度数分别是多少?
参考答案:1.C; 2.C; 3.1.85㎞;
4.因为圆弧半径为 ![]() ,
, ![]() ,
, ![]() 走过弧长为
走过弧长为 ![]() ,由公式
,由公式![]() ;
;
5. ![]() ; 6.
; 6. ![]() ,
, ![]()
板书设计
|
弧度制(二) 1.正、负、零角的弧度制意义 2.角度集合与实数集间一一对应 3.例1 |
例2 例3 |
练习反馈 小结 |