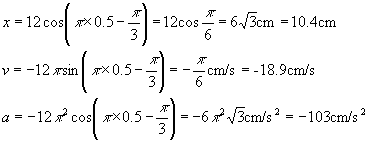第五节 相位

典型例题

　　例题1：有两个振动的振动方程分别是：

　　 ，下列说法正确的是（　）

　　A．它们的振幅相同

　　B．它们的周期相同

　　C．它们的相差恒定

　　D．它们的振动步调一致

　　出题目的：巩固并掌握简谐运动方程中各物理量的意义。

　　解析：依据两个振动方程我们知道：

　　方程1代表的振子振动振幅为3；圆频率为ω=2πf=100π，则f=50；初相为。

　　方程2代表的振子振动振幅为5，圆频率为ω=2πf=100π，则f=50；初相为π/4。

　　所以，答案A错；B对；由于他们的振动周期相同的所以他们的相位差为π/3-π/4有确定的值，故选项C正确.

　　选项D不对，由于他们的相位差为π/3-π/4=π/12，因此他们在振动时步调不一致。只有两个频率相同的振动，且相位差 时，他们的振动步调才会一致，这就是我们常说的同相；若 ，说明这两个振动正好相反，我们叫它反相.

　　例题2：两个简谐运动分别

　　 ．求它们的振幅之比，各自的频率，以及它们的相位差．

　　出题目的：巩固对简谐运动方程的基本理解.

　　解析：振幅之比 。它们的频率相同，都是 。它们的相位差 ，而振动为反相．

　　例题3：一物体沿x轴做简谐运动，振幅为8cm，频率为0.5Hz，在t＝0时，位移是4cm，且向x轴负方向运动，试写出用正弦函数表示的振动方程 ．

　　出题目的：掌握由简谐振动的各物理量，写出其振动方程的方法.

　　解析：简谐运动振动方程的一般表达式为 ．

　　根据题给条件有：A＝0.08m， 。所以                 （m）．将t＝0时x＝0.04m代入得 ，解得初相 或 ．因为t＝0时，速度方向沿x轴负方向，即位移在减小，所以取 。

　　所求的振动方程为 （m）．

　　例题4：一物体沿x轴作简谐振动。振幅为12cm，周期为2s。当 时，位移为6cm，且向x轴正方向运动。求：

　　（1）初位相；

　　（2） 时物体的位置，速度和加速度；

　　出题目的：理解简谐运动方程求解及在解题中的应用.

　　解析：由于题中已把振动的各参量给出了，只要建立振动方程，以上各问就不难通过数学方法得出。

　　解：（1）设这简谐振动的表达式为

　　

　　因为 时， 代入上式得

　　

　　解得 

　　因这时物体向x轴正方向运动，故应取

　　（2）由上述结果可得

　　

　　在 时，从上面各方程式可求得

　　

返回页首