 设为首页
设为首页
 加入收藏
加入收藏
典型例题
例1、圆内接四边形ABCD中,∠A、∠B、∠C的度数的比是3﹕2﹕7,求四边形各内角度数.
解:设∠A、∠B、∠C的度数分别为3x、2x、7x.
∵ABCD是圆内接四边形.∴∠A +∠C=180°即3x+7x=180°,
∴x=18°,
∴∠A=3x=54°,∠B=2x=36°,∠C=7x=126°,
又∵∠B+∠D=180°,
∴∠D=180°一36°=144°.
说明:①巩固性质;②方程思想的应用.
例2、(2001厦门市,教材P101中17题)如图, 已知AD是△ABC的外角∠EAC的平分线,AD与三角形ABC的外接圆相交于D.求证:DB=DC.
已知AD是△ABC的外角∠EAC的平分线,AD与三角形ABC的外接圆相交于D.求证:DB=DC.
分析:要证DB=DC,只要证∠BCD=∠CBD,充分利用条件和圆周角的定理以及圆内接四边形的性质,即可解决.
证明:∵AD平分∠EAC,∴∠EAD =∠DAC,
∵∠EAD为圆内接四边形ABCD的外角,∴∠BCD=∠EAD,
又∠CBD=∠DAC,
∴∠BCD=∠CBD,∴DB=DC.
说明:角相等的灵活转换,利用圆内接四边形的性质作桥梁.
例3、如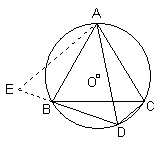 图,△ABC是等边三角形,D是
图,△ABC是等边三角形,D是 ![]() 上任一点,求证:DB+DC=DA.
上任一点,求证:DB+DC=DA.
分析:要证明一条线段等于两条线段的和,往往可以“截长”和“补短”法,本题两种方法都可以证明.
证明: 延长DB至点E,使BE=DC,连AE.
在△AEB和△ADC中,BE=DC.
△ABC是等边三角形.∴AB=AC.
∵ 四边形ABDC是⊙O的内接四边形,
∴∠ABE=∠ACD.
∴△AEB≌△ADC.
∴∠AEB=∠ADC=∠ABC.
∵∠ADE=∠ACB,
又 ∵∠ABC=∠ACB=60°,
∴∠AEB=∠ADE=60°.
∴△AED是等边三角形,∴AD=DE=DB+BE.
∵BE=DC,∴DB+DC=DA.
说明:本例利用“截长”和“补短”法证明.培养学生“角相等的灵活转换”能力.在圆中,圆心角、圆周角、圆内接四边形的性质构成了角度相当转换的一个体系,应重视.