 设为首页
设为首页
 加入收藏
加入收藏
典型例题
例1、已知两圆半径之比是5:3,如果两圆内切时,圆心距等于6,问当两圆的圆心距分别是24、5、20、0时,相应两圆的位置关系如何?
解:设大圆半径R=5x
∵两圆半径之比为5: 3,∴小圆半径r=3x,
∵两圆内切时圆心距等于6,∴5x-3x=6,∴x=3,
∴大圆半径R=15,小圆半径r=9,
当两圆圆心距dl=24时,有dl=R+r,∴此时两圆外切;
当两圆圆心距d2=5时,有d2<R-r, ∴此时两圆内含;
当两圆圆心距d3=20时, 有R-r<d3<R+r, ∴此时两圆相交;
当两圆圆心距d4=0时,两圆圆心重合,两圆为同心圆.
说明:此题考察学生对两圆位置的数量认识与形象思维的联想能力.考察数形结合能力.
例2、已知两相交 圆的半径分别为5cm和4cm,公共弦长为6cm,求这两圆的圆心距.
圆的半径分别为5cm和4cm,公共弦长为6cm,求这两圆的圆心距.
解:分两种情况:
(1)如图1,设⊙O1的半径为r1=5cm,⊙O2的半径为r2=4cm.
圆心Ol,02在公共弦的异侧.
∵O1 O2垂直平分AB,∴AD=![]() .
.
连O1A、O2A,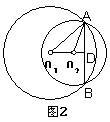 则
则![]() .
.
![]() .
.
![]() (cm).
(cm).
(2) 如图2,圆心Ol,02在公共弦AB的同侧,同理可求
01D=4cm,02D=![]() (cm).
(cm).![]() (cm).
(cm).
说明:①此题为基本题目;②此题未给出图形,所以应分两种情况求解;若题中给出图形,按已知图形分析求解即可;若题中已知的相交两圆是等圆时,两相交等圆的圆心只能在公共弦两侧.
例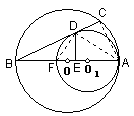 3、(武汉市,2002)已知:如图,⊙O和⊙O1内切于A,直线OO1交⊙O于另一点B,交⊙O1于另一点F,过B点作⊙O1的切线,切点为D,交⊙O于C点,DE⊥AB垂足为E.求证:
3、(武汉市,2002)已知:如图,⊙O和⊙O1内切于A,直线OO1交⊙O于另一点B,交⊙O1于另一点F,过B点作⊙O1的切线,切点为D,交⊙O于C点,DE⊥AB垂足为E.求证:
(1)CD=DE;
(2)若将两圆内切改为外切,其他条件不变,(1)中的结论是否成立?请证明你的结论.
证明:(1)连结DF、AD,
∵AF为⊙O1的直径,∴FD⊥AD,又DE⊥AB,
∴∠DFE=∠EDA,
∵BC为⊙O1的切线, ∴∠CDA=∠DFE,
∴∠CDA=∠DFE,
∴∠CDA=∠EDA,
连结AC,∵AB为⊙O的直径,
∴AC⊥BC,又AD公共,
∴Rt△EDA≌Rt△CDA,
∴CD=DE.
(2)当两圆外切时,其他条件不变,(1)中的结论仍成立.证法同(1).
说明:①此题应用“如果两个圆相切,那么切点一定在连心线上”、双垂直、弦切角、全等三角形等知识;②第(2)问是开放性问题.
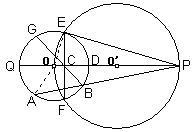
例4、(宁波市,2002)如图,⊙O’经过⊙O的圆心,E、F是两圆的交点,直线OO’交⊙O于点Q、D,交⊙O’于点P,交EF于点C且EF=![]() ,sin∠P=
,sin∠P=![]() .
.
(1)求证:PE是⊙O的切线;
(2)求⊙O和⊙O’的半径的长;
(3)点A在劣弧 ![]() 上运动(与点Q、F不重合),连结PA交
上运动(与点Q、F不重合),连结PA交 ![]() 于点B,连结BC并延长交⊙O 于点G,设CG=x,PA=y.求y关于x的函数关系式.
于点B,连结BC并延长交⊙O 于点G,设CG=x,PA=y.求y关于x的函数关系式.
证明:(1)连结OE,∵OP是⊙O’的直径,
∴∠OEP=90°,∴PE是⊙O的切线.
(2)设⊙O、⊙O’的半径分别r、r’.
∵ ⊙O与⊙O’ 交于E、F,
⊙O与⊙O’ 交于E、F,
∴EF⊥OO’, ![]() .
.
∴在Rt△EOC、Rt△POE中,∠OEC=∠OPE.
∴sin∠OEC= sin∠OPE=![]() ,
,
∴sin∠OEC=![]() ,即
,即![]() r,
r,
![]() ,得r=4.
,得r=4.
在Rt△POE中,sin∠OPE=![]() ,∴r’=8.
,∴r’=8.
(3)按题意画图,连结OA,∵∠OEP=90°,CE⊥OP,
∴PE2=PC·PO.又∵PE是⊙O的切线,∴PE2=PB·PA,∴PC·PO=PB·PA,
即![]() ,又∵∠CPO=∠APO,∴△CPB∽△APO,∴
,又∵∠CPO=∠APO,∴△CPB∽△APO,∴![]() ,
,
∴BC=60/PA.由相交弦定理得BC·CG=EC·CF,∴BC=15/CG,
∴PA=4CG,即y=4x(![]() ).
).
说明:此题为综合题目,主要应用:切线的判定、两圆相交的性质、勾股定理、三角函数、切割线定理及相似形等知识.