第十六节 正多边形和圆

典型例题

　　例1、选择题：

　　（1）下列叙述正确的是(　)．

　　(A)各边相等的多边形是正多边形　(B)各角相等的多边形是正多边形

　　(C)各边相等，各角也相等的多边形是正多边形　(D)轴对称图形是正多边形

　　答案（C）

　　（2）正多边形的每个内角与外角的关系是(　)．

　　(A)内角大于外角　(B)内角小于外角

　　(C)内角等于外角　(D)可能大于外角，可能小于外角，也可能等于外角

　　答案（D）

　　（3）在正三角形、正方形、正五边形、正六边形中，其中共有(　)个中心对称图形．

　　(A)0　　(B)l 　　(C)2　　(Ｄ)4

　　答案（C）．

　　说明：①巩固正多边形的概念；②在第（3）小题中，正方形和正六边形是中心对称图形，一般地，正2n边形既是轴对称图形也是中心对称图形，正2n+l边形是轴对称图形但不是中心对称图形．

　　例2、已知：如图，圆O的内接等腰三角形ABC，AB=AC，弦BD、CE分别平分∠ABC、∠ACB，BE=BC．求证：五边形AEBCD是正五边形．

　　证明：在△ABC中，

　　 ∵AB=AC，∴∠ABC=∠ACB，

　　又∵BD、CE分别平分∠ABC、∠ACB，

　　∴∠ABD=∠DBC=∠ACE=∠ECB，∴ = = = ，

　　又∵BE=BC，∴ =

　　∴点A、E、B、C、D把圆O五等分，

　　∴五边形AEBCD是正五边形．

　　说明：①此题利用第一个定理（判断正多边形）；②应用等腰三角形、角分线、圆周角等知识．

　　例3、求证：如果一个四边形有一个外接圆和一个内切圆，并且这两个圆是同心圆，那么这个四边形是正方形．

　　已知：如图，四边形ABCD内接于大圆O，且各边与小圆相切于点E、F、G、H．

　　求证：四边形ABCD是正方形．

　　证明：连结OE、OF、OG、OH．

　　∵四边形ABCD与小圆分别切于点E、F、G、H，

　　∴OE=OF= OG=OH=，且OE⊥AB、OF⊥BC、OG⊥CD、OH⊥AD．

　　∴AB=BC=CD=DA．

　　∴A、B、C、D是大圆O的四等分点．

　　∴四边形ABCD是正方形．

　　说明：①此题训练学生把文字语言转化为数学语言；②应用第一个定理、切线的性质、垂径定理等知识；③此题可以推广到边数是n的多边形．

　　例4、如图，在正六边形ABCDEF中，G是BF的中点，切GH⊥AB于H．

　　求证AH: AB．

　　证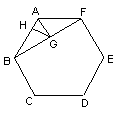明：∵AB=AF，G是BF的中点，

　　∴AG⊥BF，

　　又∠BAF= ，

　　∴∠ABG=30°=∠AGH，

　　设AH=x，则AG=2x，AB=4x．

　　∴AH:AB=x:4x=1:4

　　说明：此题应用正多边形的定义，直角三角形的有关性质．

返回页首