 设为首页
设为首页
 加入收藏
加入收藏
典型例题
例1.求同圆的内接正六边形与外切正六边形的周长比与面积比.
分析:边数相同的正多边形是相似形,因此要求同因的内接正六边形与外切正六边形的周长比与面积比,只需求出相似比(边长比、边心距比、半径比均为相似比)
解:如图,连接OA’、OA,则在△ABC中,
![]() .
.
∵OA’、OA分别为⊙O;的内接正六边形的半径和外切正六边形的半径,
∴它们的相似比=![]()
∴周长比为![]() , 面积比为
, 面积比为![]() .
.
说明:①转化为直角三角形;②同圆的内接正n边形与外切正n边形的相似比为![]() .
.
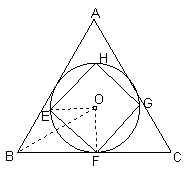
例2、如图,⊙O为正三角形ABC的内切圆,EFGH是⊙O的内接正方形,且![]() ,求正三角形的边长.
,求正三角形的边长.
分析:因为⊙O是正三角形的内切圆;又是正方形的外接,所以求⊙O 的半径成为解题的关键.
解:连结OB、OE、OF, 在等腰直角三角形OEF中,
![]() .
.
在Rt△BOF中,∠BOF=60°,OF=1,
∴BF=OF·sin60°=![]() .
.
∴BC=2BF=2![]() .
.
故正三角形的边长为2![]() .
.
说明:应用圆外切三角形和圆内接正方形的性质,构造直角三角形.
 例3、如图,⊙O的直径为AB、CD,AB⊥CD,弦MN垂直平分OB.求证:CM为正十二边形的一个边,MB为正六边形的一个边,CB正四边形的一个边,MN为正三角形的一个边.
例3、如图,⊙O的直径为AB、CD,AB⊥CD,弦MN垂直平分OB.求证:CM为正十二边形的一个边,MB为正六边形的一个边,CB正四边形的一个边,MN为正三角形的一个边.
证明:连结OM、ON
∵MN垂直平分OB,∴OM=MN.
∵OM=OB,
∴△OBM为等边三角形.
∴∠MOB=60°,即360°/n=60°,
∴n=6,∴MB为正六边形的一个边.
∵AB⊥CD,∴∠COM=30°,即360°/n=30°
∴n=12,∴CM为正十二边形的一个边.
同理由∠COB=90°,得CB正四边形的一个边,∠MON=120°,得MN为正三角形的一个边.