第三节 直线与平面平行的判定和性质

典型例题

　　例1 简述下列问题的结论，并画图说明：
　　（1）直线 平面 ，直线 ，则 和 的位置关系如何？
　　（2）直线 ，直线 ，则直线 和 的位置关系如何？
　　分析：（1）由图（1）可知： 或 ；
　　　（2）由图（2）可知： 或 ．

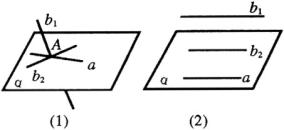
　　说明：此题是考查直线与平面位置关系的例题，要注意各种位置关系的画法与表示方法．
　　例2 是平行四边形 所在平面外一点， 是 的中点，求证： 平面 ．
　　分析：要证明平面外的一条直线和该平面平行，只要在该平面内找到一条直线和已知直线平行就可以了．
　　证明：如图所示，连结 ，交 于点 ，
　　∵四边形 是平行四边形
　　∴ ，连结 ，则 在平面 内，且 是 的中位线，
　　∴ ．
　　∵ 在平面 外，
　　∴ 平面 ．
　　说明：应用线面平行的判定定理证明线面平行时，关键是在平面内找一条直线与已知直线平行，怎样找这一直线呢？
　　由于两条直线首先要保证共面，因此常常设法过已知直线作一平面与已知平面相交，如果能证明已知直线和交线平行，那么就能够马上得到结论．这一个证明线面平行的步骤可以总结为：
　　过直线作平面，得交线，若线线平行，则线面平行．
　　例3 经过两条异面直线 ， 之外的一点 ，可以作几个平面都与 ， 平行？并证明你的结论．
　　分析：可考虑 点的不同位置分两种情况讨论．
　　解：（1）当 点所在位置使得 ， （或 ， ）本身确定的平面平行于 （或 ）时，过 点再作不出与 ， 都平行的平面；
　　（2）当 点所在位置 ， （或 ， ）本身确定的平面与 （或 ）不平行时，可过点 作 ， ．由于 ， 异面，则 ， 不重合且相交于 ．由于 ， ， 确定的平面 ，则由线面平行判定定理知： ， ．可作一个平面都与 ， 平行．
故应作“0个或1个”平面．
　　说明：本题解答容易忽视对 点的不同位置的讨论，漏掉第（1）种情况而得出可作一个平面的错误结论．可见，考虑问题必须全面，应区别不同情形分别进行分类讨论．
　　例4 平面外的两条平行直线中的一条平行于这个平面，那么另一条直线也平行于这个平面．
　　已知：直线 ， 平面 ， ．
　　求证： ．
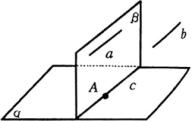
　　证明：如图所示，过 及平面 内一点 作平面 ．
　　设 ，
　　∵ ，
　　∴ ．
　　又∵ ，
　　∴ ．
　　∵ ， ，
　　∴ ．
　　说明：根据判定定理，只要在 内找一条直线 ，根据条件 ，为了利用直线和平面平行的性质定理，可以过 作平面 与 相交，我们常把平面 称为辅助平面，它可以起到桥梁作用，把空间问题向平面问题转化．
　　和平面几何中添置辅助线一样，在构造辅助平面时，首先要确认这个平面是存在的，例如，本例中就是以“直线及直线外一点确定一个平面”为依据来做出辅助平面的．
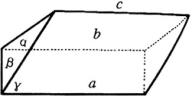　　例5 如图4所示，已知平面 平面 ，平面 平面 ，平面 平面 ， ，求证， ．
　　分析：要证 ，只须证明 和 ．又已知条件中有线面平行，这就要求我们将线面平行转化为线线平行．
　　证明：∵ ， 是过 的平面， ，∴ 同理 ，∴ ．
　　说明：直线和平面的平行问题，常常转化为直线和直线的平行问题，而直线和直线的平行问题也可以转化为直线和平面的平行问题．如遇到线线平行的问题可以想想线面平行的问题，要做出命题的正确转化，就必须熟记线面平行的定义、判定定理和性质定理的内容，明确定理中的条件和结论．解题时，分析已知和结论，通过定理的恰当运用实现转化．