 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
动量守恒定律的一个重要结论及应用
牛顿定律告诉我们一个物体所受合外力为零,则其质心(即质量中心,一般认为与重心重合)就保持静止或匀速直线运动状态不变,由此可推广到物体系统上去,一个系统所受合外力为零,尽管其内力发生相互作用,谷物体运动状态不同,但系统的质心应保持静止或匀速直线运动状态不变.
当一个系统受到合外力为零时,系统的总动量守恒,系统重心的速度将保持不变.若系统在某一方向中受到的合外力为零,则系统在该方向上的动量守恒,系统的重心在这一方向上的速度不变,这是关于动量守恒的一个重要结论.用这一结论去解决某些问题,会显得十分简便.
【例1】如图,光滑的木板AB水平放置,左端用一光滑铰链固定在墙上,右端用一轻绳挂在天花板,板上放着木块M和m,M和m之间用轻弹簧相连结,开始,弹簧被压缩,M和m之间用细绳拉住,并处于静止状态.细线剪断后,M和m在板上来回振动.问细线OB的拉力将如何变化?
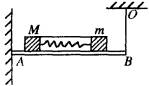
解析M和m组成的系统满足动量守恒条件,因为系统原来处于静止状态,重心速度为零,虽然后来M和m都做来回振动,但系统的重心速度仍然为零,重心位置不变,故M和m对木板的作用力所产生的对A点的总力矩不变,所以细线OB的拉力也不会变化.
【例2】如图所示,质量为m的小孩站在质量为M的小车的右端,处于静止状态,已知车的长度为l则当小孩走到小车的左端时,小车将向右移动多少距离?(忽略小车运动时受到的阻力)
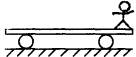
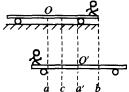
解析如图所示,设小车的重心在a线上,人的重心原来是在b线上,系统的重心在c线上,a、c的间距为x,则有 ![]() ,所以
,所以 ![]() .因为系统原来静止,受到的合外力为零,则系统重心的速度为零,重心位置设有移动,人走到小车的左端时,根据对称性车的重心将向右移动a处,移动的距离
.因为系统原来静止,受到的合外力为零,则系统重心的速度为零,重心位置设有移动,人走到小车的左端时,根据对称性车的重心将向右移动a处,移动的距离 ![]() .
.
【例3】如图是表示质量为M的密闭气缸置于光滑水平面上,缺内设一隔板P,隔板右是真空,隔板左是质量为m的高压气体,若将隔板突然抽去,则气缸的运动情况是( )
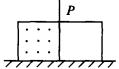
A.保持静止不动
B.向左移动一定距离后回复静止
C.向左移动一定距离后继而做匀速直线运动
D.先向左移动,后向右移动回到原来位置
解析抽去隔板前后,系统所受合外力皆为零,因此系统合质心位置始终保持不变,抽去隔板以后,气体向右扩散,气体质心右移,为保持系统合质心位置不变,气缸质心必左移,当整个气缸充满了气体而停止扩散时,气缸也就停止了向左的移动而静止,应选B.
扩展资料
动量守恒定律公式及注意事项
对任意两个物体组成的系统,不管其速度方向如何,只要在同一条直线上,动量定恒定律可表示为:
![]()
式中 ![]() 和
和 ![]() 分别是两个物体的质量,
分别是两个物体的质量, ![]() 和
和 ![]() 分别是它们原来的速度,
分别是它们原来的速度, ![]() 和
和 ![]() 分别是它们相互作用后的速度.
分别是它们相互作用后的速度.
注意:
(1)动量守恒定律的适用条件是:两个或几个物体组成的系统所受外力(即系统之外的其他物体对系统内任一物体的作用力)的合力为零,或是可以忽略.只有在这个条件下系统的总动量才守恒;
(2)动量守恒定律是自然界最重要最普遍的规律之一,大到星球的宏观系统,小到基本粒子的微观系统,无论系统内各物体之间相互作用是什么力,如万有引力、弹力、摩擦力、电力、磁力、核力等,只要满足上述适用条件,动量守恒定律都是适用的.
(3)动量是矢量,动量守恒定律是矢量方程式,必须按矢量法则进行运算.
(4)动量守恒定律和牛顿运动定律是完全一致的,但当系统内受力情况不明,或互相作用为变力时,用牛顿第二定律计算很繁杂,而动量定恒定律只管发生相互作用前、后的状态,而不必过问相互作用的细节,因而避免了直接运用牛顿定律的困难,使问题简化.
扩展资料
解题方法和技巧
动量守恒定律类型习题:由于这定律是自然界最重要最普通的规律之一.因而这类型的习题非常丰富.
应用动量守恒定律解题方法和步聚为
(1)确定所研究的物体系:注意这里区别于应用动量定理解题,不是选定某单个物体为对象,而是以两个或两个以上相互作用的物体系为对象,并分析此物体系是否满足动量守恒的条件.即这物体系是否不受外力作用,或合外力为零(或近似为零).显然物体系内力(即系内物体相互作用)仍然存在,这些相互作用内力,使每个物体的动量变化,但这物体系的总动量守恒.
(2)建立坐标,选定方向:如果所研究的物体系中每个物体的动量都在同一直线上,则须选定某方向为正向.以判断每个速度的正负;如果这些动量不是在同一直线上,则必须建立一个直角的坐标系xy,并把各个速度进行正交分解,此时,只要某一个方向上(x方向或y方向)系统不受外力或合外力投影为零时,则有
![]()
![]()
(3)确定参考系:如果所研究的物体系中的物体在做相对运动,此时应特别注意选定某一静止或作匀速直线运动的物体作为参考系,定律中各项动量都必须是对此同一参考系的速度.
(4)建立方程,求解作答:按以上正确地确定了相互作用前后速度的正负和大小后,建立起正确的方程.
![]()
保持方程两边单位一致的前提下,代入数据,进行求解作答。
扩展资料
应用动量守恒应该注意的问题
A.两个物体组成的系统,其动量守恒定律的表达式 ![]() 等号左边为相互作用过程中某时刻(t)系统的总动量.等号右边为另一时刻(
等号左边为相互作用过程中某时刻(t)系统的总动量.等号右边为另一时刻( ![]() )系统的总动量.在具体列方程时,一定要注意
)系统的总动量.在具体列方程时,一定要注意 ![]() 、
、 ![]() (可能还有
(可能还有 ![]() 、
、 ![]() …)的同时性,
…)的同时性, ![]() 、
、 ![]() (可能还有
(可能还有 ![]() 、
、 ![]() )的同时性.
)的同时性.
B.动量守恒定律公式中的速度都是相对于同一静止的事保系,如果固中给出的速度是物体间相对速度,则要把它变换成相对同一参照物的速度.
C.动量守恒定律的表达式
![]() 是矢量式.如果系统内物体间发生正碰,各物体在相互作用前、后的动量方向都在同一直线上,可规定一个正方向,用正、负号表示各物体相互作用前后动量的方向,将矢量运算简化成代数运算.
是矢量式.如果系统内物体间发生正碰,各物体在相互作用前、后的动量方向都在同一直线上,可规定一个正方向,用正、负号表示各物体相互作用前后动量的方向,将矢量运算简化成代数运算.