设为首页
设为首页
 加入收藏
加入收藏
扩展资料
光在大气中的折射
光在到达大气与透明物体的分界面,或者光在到达密度不同的两层大气的分界面时,会发生传播方向的屈折,我们把这种现象称之为光的折射.光的折射遵从折射定律.
气象学告诉我们,空气的密度的大小主要受气压和气温两个条件的影响.气压指得是单位面积空气柱的重量.大气层包围在地球表面,因此在大气层的低层气压较高,越向上气压越低.气压高则空气密度大,气压低则空气密度小.因此,正常情况下,总是贴近地面的空气密度最大,越向上空气密度越小.温度对空气密度的影响和气压则刚好相反.气温越高,空气的体积越膨胀,空气的密度越小;温度越低,空气收缩,则空气的密度变大.一般越接近地面温度越高(逆温层是个例外).根据实测所得,在大多数情况下,温度的上下差别不是太大,而气压上下的差别却很显著,因此气压对空气密度的垂直分布所产生的影响远比气温的影响大,这就使得空气密度经常是越向上越小的(当然减小的情况并不是一成不变的).
由于地球上空气的密度随高度的变化,折射率随密度减小而正比例地减小,因此光在大气中传播时,通过一层层密度不同的大气,在各层的分界面处会发生折射,使光线不沿直线传播而是变弯曲,这样当太阳和其他星体的光线进入大气以后,光线就会拐弯,这种现象称天文折射,这使在地面观测得的天体视位置S'比实际位置S高.

来自大气某目标物发出的光线,在向接收器传播途中发生屈折的现象称地球折射.
当大气中温度的垂直分布出现异常时,就会引起空气密度垂直变化异常因而产生异常折射.如果下层空气比上层空气冷,也就是出现了强烈的温度逆增时,光线在这种气温随高度升高因而使空气密度随高度锐减的气层中传播,会向下屈折;而光线在气温随高度而降低的气层内传播,会向上屈折.实际大气温度的垂直分布复杂多变,因而会产生丰富多彩的大气光象.
扩展资料
光学的重要分支——几何光学
几何光学是研究光的直线传播的科学,它以光的直线传播及光的反射定律和折射定律为理论基础,引入光线的概念,运用几何学的研究方法.而人们探索光的折射定律竟花费了1000多年的时间.公元2世纪希腊人托勒密研究了折射现象,写了《光学》一书.书中记载了他通过实验测定的光由空气进入水中时,对应于不同的入射角所产生的折射角,根据他的实验,托勒密认为折射角和入射角成正比.虽然结论并不正确,但他是第一个用实验定量的研究折射现象的人.随后有荷兰人斯涅耳和法国人笛卡尔对折射现象进行了更为精细的定量的实验研究,分别发现了具有现代形式的光的折射定律.
对物理现象进行精确的定量研究,才使之发展成为一门实验科学,随后将数学引进来,使之进一步理论化,使物理学具有了今天的面目.
光的折射定律和光的反射定律为几何光学奠定了基础.为了扩大人的观察能力,荷兰人李普赛制作出第一架望远镜,后经意大利人伽利略的研究,千方百计增加它的放大倍数,创制了用凸透镜做物镜,用凹透镜做目镜的伽利略望远镜.他的不朽的功勋之一是第一个把望远镜指向天空,当时的目的是为了证实哥白尼的日心说.他得到了比预期更好的效果,发现了大量用肉眼看不见的新星;证明了银河是由大量极小的星星汇集而成;发现了月球上存在山和凹地,并于1610年用放大率为30倍的望远镜观察到木星的四个卫星,它们好像月亮绕地球转动一样绕木星转动.这些观察到的事实,就完全证实了哥白尼学说的正确性.
扩展资料
精确折射定律的最早发现者——斯涅耳
威里布里德.斯涅耳(Willebrord Snell Van Roijen 1591-1626),荷兰莱顿人,数学家和物理学家,曾在莱顿大学担任过数学教授.斯涅尔最早发现了光的折射定律,从而使几何光学的精确计算成为了可能.

一、前人对光折射的研究
古希腊人最早对光现象进行数学处理,欧几里德在他的《光学》里总结了到他那时为止已有的关于光现象的知识和猜测.那时的人们已经知道,在眼睛和被观察物体之间行进的光线是直线;当光线从一个平面反射时,入射角和反射角相等.在这个时期,折射现象虽已为人所知,但还属于经验上的讨论.
古希腊科学典籍中关于光折射的实验记载寥寥无几,最早的应该是公元二世纪托勒密所做的光的折射实验.他在一个圆盘上装两把能绕盘心旋转的尺子,将圆盘的一半浸入水中.让光线由空气射入水中,就得到它在水中的折射光线,转动两把尺子,使它们分别与入射光线和折射光线重合.然后取出圆盘,按尺子的位置刻下入射角和折射角.他所测出的一系列数据是非常精确的.托勒密大致假定了光的入射角和折射角之间,有一直接的比例关系.托勒密依靠经验发现了折射的规律,但却没有由此得出精确的折射定律.
1609年,伽利略制成了望远镜,并利用他进行了很多科学观测.这些新的发现激励开普勒对光折射现象进行了深入的研究,并于1611年出版了《折射光学》一书.开普勒的研究表明,对于两种给定的媒质,小于30度的入射角同相应的折射角成近似固定的比,对于玻璃或水晶,这个比约为3:2.他还表明,这个比对于大的入射角不成立.开普勒试图通过实验发现精确的折射定律,他的方法虽然是正确的,却没有得到其中有规律性的联系.但是,开普勒的研究为后来斯涅耳得出折射定律起到了一定的启示作用.
二、折射定律的得出
大约是在1621年,斯涅耳通过实验确立了开普勒想发现而没有能够发现的折射定律.当时斯涅耳注意到了水中的物体看起来象漂浮的现象,并试图揭开其中的奥秘.由此便引出了他对折射现象的研究.
在总结托勒密、开普勒等前人的研究成果后,斯涅耳做了进一步的实验.在实验中,斯涅耳应用开普勒的方法发现:从空气到水里并落在容器垂直面上的一条光线在水中所走的长度,同该光线如按未偏离其原始方向而本来会通过的路程成一定的比.他指出:折射光线位于入射光线和法线所决定的平面内,入射光线和折射光线分别位于法线两侧,入射角的正弦和折射角的正弦的比值对于一定的两种媒质来说是一个常数.这个常数是第二种媒质对第一媒质的相对折射率,即: ![]() ,
, ![]() .其中
.其中 ![]() 和
和 ![]() 分别为入射角和折射角;
分别为入射角和折射角; ![]() 为折射光所在媒质对入射光所在媒质的相对折射率;
为折射光所在媒质对入射光所在媒质的相对折射率; ![]() 和
和 ![]() 为两种媒质的绝对折射率.斯涅耳的这一折射定律(也称斯涅耳定律)是从实验中得到的,未做任何的理论推导,虽然正确,但却从未正式公布过.只是后来惠更斯和伊萨克·沃斯两人在审查他遗留的手稿时,才看到这方面的记载.
为两种媒质的绝对折射率.斯涅耳的这一折射定律(也称斯涅耳定律)是从实验中得到的,未做任何的理论推导,虽然正确,但却从未正式公布过.只是后来惠更斯和伊萨克·沃斯两人在审查他遗留的手稿时,才看到这方面的记载.
首次把折射定律表述为今天的这种形式的是笛卡儿,他没做任何的实验,只是从一些假设出发,并从理论上推导出这个定律的.笛卡儿在他的《屈光学》(1637)一书中论述了这个问题.
折射定律是几何学的最重要基本定律之一.斯涅耳的发现为几何光学的发展奠定了理论基础,把光学发展往大大的推进了一步.
三、斯涅耳的数学成就
斯涅耳在数学上也颇有成就.他善于实验和测量.1617年,他运用三角方法,精确地测量了地球的大小,且测出了纬度一度为66.66英国法定里.他得出的这一数据比前人的数据精确的多,所以后来被引用在《函数尺和直角仪的说明》以及《地理学》等书中.
扩展资料
实验:测定玻璃的折射率知识点
【实验目的】
测定玻璃的折射率,学习一种测定固体折射率的方法.
【实验原理】
如图所示,要确定通过玻璃砖的折射光线,通过插针法找出跟入射光线 ![]() 对应的出射光线
对应的出射光线 ![]() ,就能求出折射光线
,就能求出折射光线 ![]() 和折射角
和折射角 ![]() .再根据折射定律就可计算玻璃的折射率:
.再根据折射定律就可计算玻璃的折射率:
![]()

【实验器材】
玻璃砖一块;白纸;木板;大头针;图钉;三角板;量角器;铅笔.
【实验步骤】
1、把白纸用图钉钉在木板上.
2、在白纸上画一条直线
![]() 作为玻璃砖的上界面,画一条线段
作为玻璃砖的上界面,画一条线段 ![]() 作为入射光线,并过
作为入射光线,并过 ![]() 点画出界面
点画出界面 ![]() 的法线
的法线 ![]() .
.
3、把长方形的玻璃砖放在白纸上,使它的一个长边跟
![]() 严格对齐,并画出玻璃砖的另一个长边
严格对齐,并画出玻璃砖的另一个长边 ![]() .
.
4、在
![]() 线段上竖直地插上两枚大头针
线段上竖直地插上两枚大头针 ![]() 、
、 ![]() .
.
5、在玻璃砖的
![]() 一侧竖直地插上大头针
一侧竖直地插上大头针 ![]() ,调整眼睛观察的视线,要使
,调整眼睛观察的视线,要使 ![]() 恰好能挡住
恰好能挡住 ![]() 和
和 ![]() 在玻璃砖中的虚像.
在玻璃砖中的虚像.
6、用同样的方法在玻璃砖的
![]() 一侧再插上大头针
一侧再插上大头针 ![]() 、使
、使 ![]() 能同时挡住
能同时挡住 ![]() 本身和
本身和 ![]() 、
、 ![]() 的虚像.
的虚像.
7、记下
![]() 、
、 ![]() 的位置,移去玻璃砖和大头针.过
的位置,移去玻璃砖和大头针.过 ![]() 、
、 ![]() 引直线
引直线 ![]() 与
与 ![]() 交于
交于 ![]() 点,连接
点,连接 ![]() 、
、 ![]() ,
, ![]() 就是入射光
就是入射光 ![]() 在玻璃砖内的折射光线的方向.入射角
在玻璃砖内的折射光线的方向.入射角 ![]() =∠
=∠ ![]() ,折射角
,折射角 ![]() =∠
=∠ ![]() .
.
8、用量角器量出入射角
![]() 和折射角
和折射角 ![]() .
.
9、从三角函数表中查出入射角和折射角的正弦值,记入自己设计的表格里.
10、用上面的方法分别求出入射角是15°、30°、45°、60°和75°时的折射角.查出入射角和折射角的正弦值,把这些数据也记在表格里.
11、计算出不同入射角时
![]() 的值.比较一下,看它是否接近一个常数.求出几次实验中测的
的值.比较一下,看它是否接近一个常数.求出几次实验中测的
![]() 的平均值,就是玻璃的折射率.
的平均值,就是玻璃的折射率.
【注意事项】
1、用手拿玻璃砖时,手只能接触玻璃砖的毛面或棱,不能触摸光洁的光学面.严禁把玻璃砖当尺子画玻璃砖的两个边
![]() 、
、 ![]() .
.
2、实验过程中,玻璃砖在纸上的位置不可移动.
3、大头针应竖直地插在白纸上,且玻璃砖每一侧的两枚大头针
![]() 和
和 ![]() 间、
间、 ![]() 和
和 ![]() 间的距离应尽量大一些,以减少确定光路方向时造成的误差.
间的距离应尽量大一些,以减少确定光路方向时造成的误差.
4、实验时入射角不宜过小,否则会使入射角和折射角的值偏小,增大测量误差;入射角也不宜过大,否则在
![]() 一侧要么看不到
一侧要么看不到 ![]() 、
、 ![]() 的虚像,要么看到
的虚像,要么看到 ![]() 、
、 ![]() 的像模糊不清,并且变粗,不便于插大头针
的像模糊不清,并且变粗,不便于插大头针 ![]() 、
、 ![]() .
.
5、由于要多次改变入射角的大小重复实验,所以入射光线与出射光线要一一对应编号以免混乱.
【误差分析】
本实验对结果影响最大的是测量光在玻璃中的折射角r的误差.应采取以下措施减小误差:
1、选用宽度
![]() 较大的玻璃砖,宜在5cm以上.
较大的玻璃砖,宜在5cm以上.
2、入射角应在15°~75°范围内取值.
3、在纸上画
![]() 、
、 ![]() 两条线时,应尽量准确地与玻璃砖的两个平行的折射面重合,这样,两交点
两条线时,应尽量准确地与玻璃砖的两个平行的折射面重合,这样,两交点
![]() 、
、 ![]() 才能与光线的实际入射点较好地相符,否则将使画出的玻璃中折射光路与实际情况严重偏离.
才能与光线的实际入射点较好地相符,否则将使画出的玻璃中折射光路与实际情况严重偏离.
4、大头针
![]() 、
、 ![]() 的位置应靠近玻璃砖,最好由两人同时分别由
的位置应靠近玻璃砖,最好由两人同时分别由 ![]() 、
、 ![]() 端观察校正插针的位置.
端观察校正插针的位置.
5、画图要用细铅笔,力求精确.
6、为避免由于测量入射角
![]() 、折射角
、折射角 ![]() 所造成的误差,以及由于多次查数学用表所带来的麻烦,我们还可以用取不同的入射角时计算
所造成的误差,以及由于多次查数学用表所带来的麻烦,我们还可以用取不同的入射角时计算
![]() 值来证明了折射定律的成立,同时又方便地求出了玻璃的折射率.
值来证明了折射定律的成立,同时又方便地求出了玻璃的折射率.
7、本实验也可以不用平行板玻璃砖、实验的关键在于用插针法确定射出玻璃砖的出射光线,然后通过连接入射点和出射点找到折射光线.
扩展资料
从“光的折射定律”探讨研究性教学设计的有关问题
徐月明
(浙江教育学院 浙江,杭州 310012)
摘要:通过“光的折射定律”作为课例来探讨研究性教学的设计.从观察、实验到数据归纳、抽象得到物理定律;从解释自然现象、技术应用到揭示物理思想和物理本质,并以此提出新的预言、推论,解释新现象.把提供教学资源和探究性教学策略相结合,从而实现研究性教学的目标.
关键词:研究性教学;物理学史;光的折射;物理模型
物理研究性教学把培养创新精神、研究能力和实践能力作为目标取向,根据科学研究的一般的基础的方法,通过连续观察、提出问题、进行实验、探索分析等过程,对教学内容进行研究性教学活动,掌握物理知识,培养学生科学态度和价值观、创新精神和创新思维及创新能力,提高实践操作、解决生活中与物理学习相关的实际问题的能力.然而,应该看到,许多学生还不会探究,因此,与研究性学习相配合,研究性教学应该在物理教学中有其独特的地位.研究性教学的设计主要围绕“学习策略”和“学习环境”两个方面进行.本文通过“光的折射定律”来探讨研究性教学设计的有关问题.
1、从现象观察到科学实验,促使学生的现有概念向科学概念发展
(1)确立概念.设置几个现象的观察,使学生通过这些观察并进行分析,提出“光的折射”的概念.
观察1:在玻璃杯里倒入适量的水,放入一双筷子后,看上去似乎“折断”了.观察2:在空的白搪瓷杯子里放一枚五彩石,从上面斜着看,无法看到;然后往杯子里倒水,随着林中水面的升高,你不仅可以看到,而且会感觉到五彩石的位置发生了变化.观察3:取一个大口玻璃杯,盛有适量水(其中加一点红汞显示光路),用手电筒(激光束)产生一束光照到水的表面,观察附近水面光路的变化.
现象的观察只是为学生确立“光的折射”概念提供一个感性认识,而科学概念的形成从经验事实出发需要构建逻辑数学结构,因此教师还应用光路图来表示光的传播,进一步阐明“光的折射”概念(图1).这也是把原始问题中的原型抽象成物理和数学逻辑结构模型,这往往是解决原始问题的关键.


(2)光的折射实验.
现象的观察和分析为我们建立了“光的折射”的概念,但是如果深入研究现象往往需要进行科学实验,有控制的实验观察、精确有效的计量是研究的必要手段.在这里教师需组织学生进行折射实验(而不是在课后),同时可以引入物理学史中对光折射实验的情况帮助学生构建具有“逻辑数学结构”的折射定律.例如,光折射实验最早可以追溯到古希腊.据考证,约公元140年,天文学家托勒密专门做了“光从空气到水中发生‘偏折’”的实验.托勒密的实验装置如图2所示.在圆盘中心S处装了两把可以旋转的尺子,将圆盘的一半竖直插入水中,旋转两把尺子以确定入射光线和折射光线的方位,从而测出入射角和折射角.将角度列成表(表1).从这里我们可以看到没有深入的思考、分析,只有描述是无法形成物理定律的.
表1:光线对应角度
|
入射角 |
0 |
10° |
20° |
30° |
40° |
50° |
60° |
70° |
80° |
|
折射角 |
0 |
8° |
12.5° |
22.5° |
29° |
35° |
40.5° |
45.5° |
50° |
2、从实验数据中归纳、概括、抽象,是发现物理规律的重要途径
通过实验,人们可以深入观察一个现象,进行测量使我们得到了足够的实验数据;但是通过把有关的测量的数据列表进行分析,试图找出事物内在的、相联系的规律性,这是物理定律发展过程中的重要的步骤.从以上实验数据一般无法找出我们所需的规律.事实上,物理学家在1000多年后才有现在表述的“光的折射定律”.
托勒密得出实验结果后,只是从数据的表面简单寻找比例关系,因此只能得出:折射角与入射角成正比(事实上,只在小角度情况下成立).1611年开普勒对折射现象和透镜的原理作了广泛的研究,写成了《折光学》,正确地指出:只在小角度情况下,入射角与折射角成正比.同时通过光的可逆性,从反面倒推得出结论,并通过实验发现了全反射现象.但是他未能得出更一般的、内在的规律.
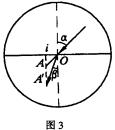
折射定律的正确表述是1621年荷兰数学家斯涅耳从实验中得到的.斯涅耳采用了与开普勒基本相同的实验方法.他在分析实验数据中发现(但没有正式发表),图3中比值有如下关系:
![]()
可以通过实验数据拟合得出n,对于水, ![]() 。通过斯涅耳折射定律,我们可以预言光从空气进入水中如何“偏折”.应该说,这是物理规律的最基本的应用,这也是物理规律的价值所在.
。通过斯涅耳折射定律,我们可以预言光从空气进入水中如何“偏折”.应该说,这是物理规律的最基本的应用,这也是物理规律的价值所在.
物理规律的产生需要运用多种数学方法:列表、图像、数学公式等等,而用一个简单的数学式(数学模型),准确地表达相关物理量的关系,是最简明的,最为理想的,因此,它成为人们追求的目标.
由此我们可以看到:①一个物理定律的得出往往经历一个漫长、曲折的过程需要坚韧的创新精神,做前人没有做过的事.因此,培养百折不挠的求真精神是教学的前提.②建立物理定律必须掌握丰富的数学知识,还需要必要的物理知识作为基础.如果没有广博的知识,根本谈不上能力.科学家之所以能在新的复杂的情况下抓住问题本质去处理问题,关键在于广博知识的迁移。
3、运用物理规律解释自然现象,拓展应用实例
中学物理教学一直重视理论知识在解释自然现象和技术中的应用,以此来体现科学的价值,激发学生深入、自主学习的兴趣.光的折射定律可以来解释许多自然界的光现象,同时也有许多实际的应用.
(1)为什么在游泳池边向池底望去,感觉池水并不深,等到下水后,才知道不是那么一回事?
(2)后面学习中要介绍的放大镜、望远镜及照相机的镜头等,都使用了透镜.透镜的功用主要是来自它对光的折射作用.
(3)全反射.根据折射定律可以推论,光从光密介质射入光疏介质时,当入射角达到临界角(折射角达到90°)时,折射光线完全消失,只剩下反射光线(图4),可以计算得结果如表2所示.
表2
|
n |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
1.9 |
2.0 |
|
|
50° |
45° |
42° |
39° |
36° |
34° |
32° |
30° |
眼睛长在头顶的鱼在水中( ![]() 约49°,
约49°, ![]() )只需其向上看,就可以观察两岸上的情况.
)只需其向上看,就可以观察两岸上的情况.
全反射的应用很多,特别是光导纤维,医疗上的内窥镜,“信息高速公路”的通讯光纤等.
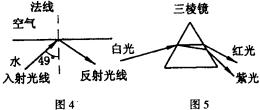
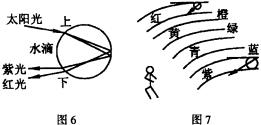
(4)色散.白光(太阳光)经折射后变成各种颜色组成的彩色光谱.“一束白光照过来,一条色带显出来.”牛顿早在几百年前就已经做过了.这是由于不同颜色的光折射率是不同的,红光折射率最小,紫光折射率最大(图5).金刚石、水晶被切割磨成若干个面就是为了无论从哪个方向射来的光线,每一个面都使光色散,发出彩色的闪光.光的色散还被用来作为“光谱分析”的工具.
(5)大气中的光学现象.例如,教材上介绍的“海市蜃楼”、雨过天晴后的“彩虹”,实际上就是太阳光受到折射而产生的彩色光谱.光线在空气中的水滴的表面受到折射,进入水滴以后,在水滴内表面又反射(图6,其他反射、折射光线未在图中示出).天空中布满小水滴,在地面上的人看来,最上面的水滴射出的光是红光,这是因为红光折射后偏低,能到达人眼,由于其余颜色的光偏高,从观察者的眼睛上方通过,所以看不到.事实上当我们看到彩虹时,不同颜色的光是从不同的水滴射来的(图7).显然,物理的学问就在我们的身边、在我们的生活中.