第十三节 圆和圆的位置关系

扩展资料

分类讨论思想

　　当面临的问题不宜用一种方法处理或同一种形式叙述时，就把问题按照一定的原则或标准分为若干类，然后逐类进行讨论，再把这几类的结论汇总，得出问题的答案，这种解决问题的思想方法就是分类讨论的思想方法．

　　分类讨论的思想方法的实质是把问题“分而治之，各个击破”．其一般规则及步骤是：(1)确定同一分类标准；(2)恰当地对全体对象进行分类，按照标准对分类做到“既不重复又不遗漏”；(3)逐类讨论，按一定的层次讨论，逐级进行；(4)综合概括小结，归纳得出结论．

　　例1、已知两相交圆的半径分别为8cm和5cm，公共弦长为6cm，求这两圆的圆心距．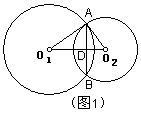

　　 解：分两种情况：

　　（1）如图1，设⊙O₁的半径为r₁=8cm，⊙O₂的半径为r₂=5cm．

　　圆心O_l，0₂在公共弦的异侧．

　　∵O₁ O₂垂直平分AB，∴AD= ．

　　连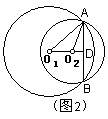O₁A、 O₂A，则．

　　 ．

　　 （cm）．

　　（2） 如图2，圆心O_l，0₂在公共弦AB的同侧，同理可求

　　0₂D=4cm，0₁D= （cm）． （cm）．

　　说明：本题要求我们自己作图计算，究竟两圆的圆心在公共弦的同侧，还是异例题设中没有交待，需要我们自己去研究．因此，凡做到没有图形的几何题时，要特别当心，有可能有几种位置形状的图形．

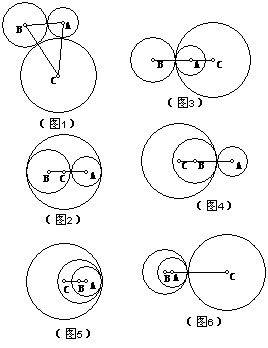
　　例2、已知：⊙A、⊙B、⊙C的半径分别为2、3、5，且两两相切，求AB、BC、CA的长

　　解：分类讨论：

　　（1）当⊙A与⊙B外切时，分4种情况：

　　①如图1，AB=5，BC=8，CA=7；

　　②如图2，AB=5，BC=2，CA=3；

　　③如图3，AB=5，BC=8，CA=3；

　　④如图4，AB=5，BC=2，CA=7；

　　（2）当⊙A与⊙B内切时，分2种情况：

　　①如图5，AB=1，BC=2，CA=3；

　　②如图6，AB=1，BC=8，CA=7．

　　说明：此题需要两次分类，但关键是以什么为标准进行分类，才能不重不漏．

返回页首