第十三节 等腰三角形的判定

典型例题

　　例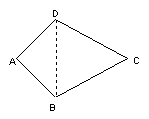1．已知：如图，AB=AD，∠B=∠D．

　　求证：CB=CD．

　　分析：解具体问题时要突出边角转换环节，要证CB=CD，通常在三角形中求解，需构造一个以 CB、CD为腰的等腰三角形，连结BD，需证∠CBD=∠CDB，但已知∠B=∠D，由AB=AD可证∠ABD=∠ADB，从而证得∠CDB=∠CBD，推出CB=CD．

　　证明：连结BD，在 中， （已知）

　　　 （等边对等角）

　　　 （已知）

　　　 即

　　　 （等角对等边）

　　小结：求线段相等一般在三角形中求解，添加适当的辅助线构造三角形，找出边角关系.

　　例2．已知：如图在△ABC中，AC=BC，∠ACB=120°CE⊥AB于D且DE=DC。

　　求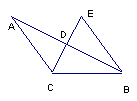证：△CEB为等边三角形。

　　分析：证明等边三角形有推论1，2两个定理依据，因此要寻找定理需要的条件.

　　证明：∵AC=BC，CE⊥AB于D

　　　∴CD平分∠ACB（等腰三角形底边的高平分顶角）

　　　∵∠ACB=120°

　　　 （角平分线）

　　　在 和 中

　　　

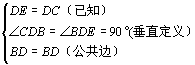
　　　 （推论2）

　　　 是等边三角形.

　　小结：也可由三个角都相等推出△CBE是等边三角形。

　　例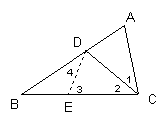3．已知：如图△ABC中∠A=2∠B、CD平分∠ACB。

　　求证：BC=AC+AD

　　分析：等量关系通常在三角形中寻找，因此经常需要构造三角形。对于线段和或差的问题通常通过截长或补短转化为线段间的等量关系。

　　证法1：（截长法）

　　　在BC上截取CE=CA连结DE。

　　　∵CD平分∠ACB

　　　∴∠1=∠2

　　　在△ACD和△ECD中

　　　

　　　

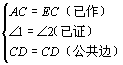
　　　 ，AD=DE

　　　

　　　

　　　

　　　

　　　 BE=DE

　　　 AD=BE

　　　 BC=BE+EC

　　　  BC=AC+AD

　　证法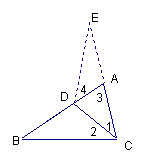2：延长CA到E，使AE=BD连结DE

　　　由条件推出△CED≌△CBD(SAS)

　　　∴CE=CB  ∠E=∠B

　　　∵∠3=2∠B

　　　∴∠3=2∠E

　　　∴∠4=∠E

　　　∴AE=AD

　　　∵EC=AC+AE

　　　∴BC=AC+AD

　　小结：对于线段之间倍半关系，常采用“截长补短”等辅助线的添加方法，或构造“倍”，或构造“半”，从而转化为线段间的等量关系.

　　例4．在 中，AB=AC, ，D是BC中点， 于E，求证：EB=3EA.

　　分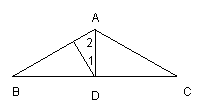析：要证EB=3EA，注意到 ，AB=AC，得 ，再证 ，得 ，若能证得 就得到 ，从而可证得EB=3EA.因此证出 中， 即可。

　　证明： （已知）

　　　 （等边对等角）

　　　又 ，

　　　在 中， ，

　　　在 中， ，

　　　 ， ，

　　例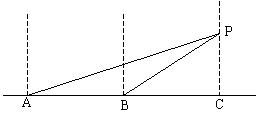5．一轮船由西向东航行，在A处测得小岛P的方位是北偏东 ，又航行7海里后，在B处测得小岛P的方位是北偏东 ，若小岛周围3.8海里内有暗礁，问该船一直向东航行有无触礁的危险。

　　分析：本题是特殊的实际问题，首先根据题意画出符合实际条件的图形，然后用数学知识来解决。因为小岛周围3.8海里内有暗礁，这样要求出小船距小岛的最短距离是大于3.8海里还是小于3.8海里。如图所示也就是求出PC的长度即可。

　　解：由题可画图，则AB＝7海里

　　过点P作PC⊥AB，垂足为C.由题中分别在A、B两测得P的方位角可知：

　　　∠PAB＝ ，∠PBC＝

　　　∴∠APB＝∠PBC－∠PAB＝

　　　∴∠PAB＝∠APB

　　　∴PB＝AB＝7

　　　在Rt△PBC中，∵∠PBC＝

　　　∴PC＝ PB＝ 7＝3.5

　　就是说C点距P只有3.5海里，而小岛P周围3.8海里内有暗礁，所以该船一直向东航行有触礁的危险.

　　小结：在平面上用角度表示方向的问题，是常见的问题.虽然在第一册中已见过一些，在这里还要进一步讲清怎样用角度表示平面内的方向问题。

　　例6．如图，在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且CE=BD，

　　求证：DF=EF

　　分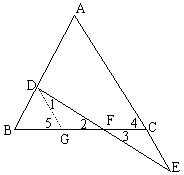析：要证DF=EF，其中DF在△BDF中，EF在△CEF中，而△BDF与△CEF不可能全等，这样需添加辅助线，由于辅助线的作法有多种情况，致使本题有多种解法。

　　证法1：过D点作DG∥AE交BC于G，

　　　则∠4＝∠5，, ∠1＝∠E，∠3＝∠2

　　　∵AB＝AC　∴∠B＝∠4　∴∠B＝∠5　∴BD＝DG

　　　∵BD＝CE　∴DG＝CE

　　　在△DFG与△EFC中

　　　

　　　∴△DFG≌△EFC

　　　∴DF=EF

　　证法2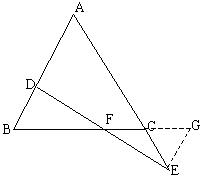：过E点作EG∥AB交BC的延长线于G，

　　　 ∠B=∠G

　　　∵AB=AC　∴∠B=∠ACB

　　　∵∠ACB=∠ECG　∴∠ECG＝∠G

　　　∴EG＝EC　∵BD＝EC　∴BD=EG

　　　在△BDF与△GEF中

　　　

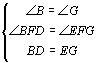
　　　∴△BDF≌△GEF

　　　∴DF=EF

　　证法3：过D点作DG⊥BC垂足为G，过E作EH⊥BC，足为H

　　则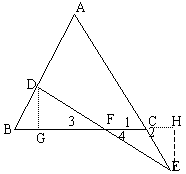∠DGB＝∠EHC=90_°，

　　　∵AB＝AC　∴∠B＝∠1　∵∠1＝∠2

　　　∴∠B＝∠1

　　　在△BDG与△CEH中，

　　　∴△BDG≌△CEH（AAS）

　　　∴DG=EH

　　　在△DGF和△EHF中，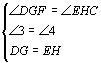

　　　∴△DGF≌△EHF（AAS）∴DF=FE

　　小结：这是一道随着辅助线的不同画法而得到多种解法的一题多解题目，有助于培养发散思维和创新思维能力。这也是本题的创新之处。

返回页首