 设为首页
设为首页
 加入收藏
加入收藏
例1.在![]() 中,已知
中,已知![]() 求
求![]() 和
和![]() .
.
分析:已知两边和其中一边的对角的解三角形问题.可运用正弦定理来求解,但应注意解的情况.或借助余弦定理,先求出![]() 后,再求出角
后,再求出角![]() 与角
与角![]() 与角
与角![]() .
.
解:解法一:![]() ∴问题有两解.
∴问题有两解.
由正弦定理,得![]()
![]()
(1)当![]() 时,
时,![]()
![]()
(2)当![]() 时,
时,![]()
![]()
故![]()
解法二:由余弦定理有![]()
即![]()
整理,得![]() 解得
解得![]()
又![]()
当![]() 时,由①可得
时,由①可得![]()
故![]() ;
;
当![]() 时,由①可得
时,由①可得![]()
故![]()
故![]()
小结:对本题,一般会误认为只能动这用正弦定理求解,而余弦定理似乎难以派上用场.其实不然,解法二就是珍上明证.
事实上,正弦定理与余弦定理是等价的,完全可以相通.凡是能用正弦定理解的三角形,用余弦定理也能求解.反之亦然,只不过解题过程的繁简程度有所不同而已.鉴此,我们在学习中,不能把正弦定理与余弦定理完合割裂开来,而要用一种联系的观点来看等待它们.
已知两边和其中一边的对角,三角形的形状一般不是确定的.若用正弦定理解这类问题时,必须根据条件判明这个三角形是否有解,有解时是一解还是两解.具体方法是:若给出的角是锐角(如本例),若这角的对边小于另一边,则有两解.反之则只有一解;若给出的角是钝角,若这角的对边大于另一边,有一解.反之则无解.显然,这种判断方法的依据就是:同一三角形中大边(角)对大角(边).
若用余弦定理解此类问题,如何来判断这个三角形是否有解,请读者自行考虑.
例2.在![]() 中,已知
中,已知![]() 求
求![]()
分析:已知三边,可用余弦定理直接求角,先求出两个角后,再用内角和求第三个角.使用余弦定理求角时,一般在判断三条边的大小后,可先求最大角,也可选求最小角,如果最大角小于60°,最小角大于60°,可知三角形无解.
解:由已知,![]() 最大.
最大.
由余弦定理,得

由正弦定理,得
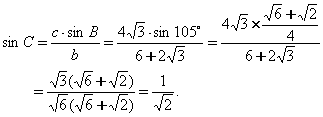
![]() 为锐角,
为锐角,![]() .
.
于是![]()
![]()
小结:此题也可由余弦定理先求最小角A,![]() 再求其他角.由于题目已知三边,所以利用余弦定理求得最大角或最小角后,再求第二个角,仍可用余弦定理,例如由
再求其他角.由于题目已知三边,所以利用余弦定理求得最大角或最小角后,再求第二个角,仍可用余弦定理,例如由![]()
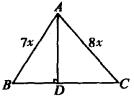 例3.如图所示,在
例3.如图所示,在![]() 中,已知
中,已知![]() 求
求![]() 边上的高.
边上的高.
分析:由已知设AB=7x,AC=8x,故要求AD的长只要求出x,△ABC中已知三边只需再有一个角,根据余弦定理便可求x,而用正弦定理正好可求角C.
解: 在△ABC中,设AB=7x,AC=8x.
由正弦定理得![]()
![]() 舍去,否则由
舍去,否则由![]() 知B也为钝角,不合要求).
知B也为钝角,不合要求).
再由余弦定理得![]()
![]()
在![]() 中,
中,![]()
![]()
小结:利用比例式的设法是一种解题常用的技巧,可使运算简便.
例4.已知方程![]() 的两根之积等于两根之和,且
的两根之积等于两根之和,且![]() 为
为![]() 的两边,
的两边,![]() 为两内角,试判定这个三角形的形状.
为两内角,试判定这个三角形的形状.
分析:先由已知条件得出三角形的边角关系.要判定三角形的形状,只须将边角关系转化为边之间或角之间的关系即可判定.
解:解法一:设方程的两根为![]() ,由韦达定理知:
,由韦达定理知:
![]()
由题意有![]()
根据余弦定理得

化简得![]()
∴ ![]() 为等腰三角形.
为等腰三角形.
解法二:仿(1)得
![]()
由正弦定理得:
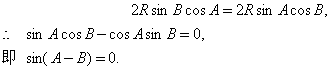
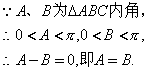
故![]() 为等腰三角形.
为等腰三角形.
小结:由三角形的边角关系判定三有的形状,其本思路是根据正弦定理和余弦定理进行边角变换,或全化为边的关系、或全化为角的关系,然后利用简单的平面几何知识即可判定.
例5.在![]() 中,
中,![]() 求证:
求证:![]() 成等差数列.
成等差数列.
分析:本例的已知条件是边角关系式,要证的是边的关系.可以考虑把已知条件化为边的关系,也可以考虑把已知条件化为角的关系先进行化简,然后再转化为边的关系.
证法一:
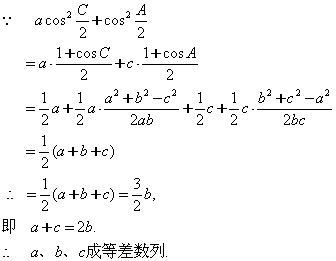
证法二:
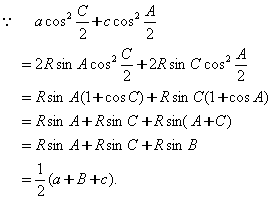
以下同证法一.
小结:三角形中边角关系恒等式的证明,主要是根据正、余弦定理,或者全化为边的关系转化为代数问题处理,或者全化为解的关系转化为三角问题处理.
例6 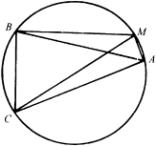 .如图,在
.如图,在![]() 中,
中,![]() 分别为角
分别为角![]() 的对边,
的对边,![]()
![]() 是
是![]() 外接圆的直径,
外接圆的直径,![]() 求
求![]() 的长.
的长.
分析:要求出三角形外接圆直径长,根据正弦定理,只要求出![]() 的一个内角和它的对边.由题设等式的特点,利用余弦定理可求
的一个内角和它的对边.由题设等式的特点,利用余弦定理可求![]() ,接着它的对边
,接着它的对边![]() 在
在![]() 中可求,问题得到解决.
中可求,问题得到解决.
解:由余弦定理:

在![]() 中,由余弦定理,
中,由余弦定理,
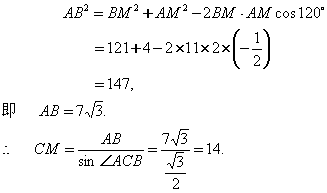
小结:在较为复杂的图形中求边或角,首先要找出有关的三角形,合理使用正弦定理或余弦定理.