 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例
一.教学目标
1.会用计算器求数的立方根.
2.通过用计算器求立方根,培养学生的类比思想,提高运算能力;
3.利用计算器求立方根,使学生进一步领会数学的转化思想;
4.通过利用计算器求值体验现代科技产品迅速、精确的功能,激发学习、探索知识的兴趣。
二.教学重点与难点
教学重点:用计算器求一个数的立方根的程序
教学难点:准确的用计算器求一个数的立方根
三.教学方法
启发式
四.教学手段
计算器,实物投影仪
五.教学过程
前面我们学习了用计算器求一个数的平方根,现在我们回忆一下计算器的使用方法.如何利用计算器求一个数的平方根?操作步骤?
练习:求下列各数的平方根:
(1)13; (2)23.45
在初一学习了用计算器求一个数的平方或立方的方法?(由学生回答操作过程,并对比两者的差别与联系)
对于用计算器求一个数的平方根的方法我们已经熟悉了,那么如何用计算器器其一个数的立方根?与求平方根有何区别和练习?
对于求立方根和平方根的操作过程基本相同,主要差别是在开方的次数上,因此要注意其立方根时开方数是3。
例1.用计算器求![]()
分析:求解时要用到![]() 上方的键
上方的键![]() ,因此要用到“2F”功能键转换。
,因此要用到“2F”功能键转换。
解:用计算器求![]() 的步骤如下:
的步骤如下:
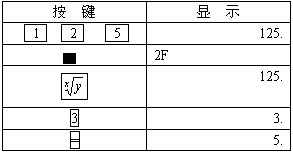
![]()
![]() =5
=5
小结:从这道题刻一个观察出用计算器求立方根和平方根十分类似,区别是在倒数第二步的按键将 ![]() 改为改为
改为改为 ![]() ,只是次数不同。
,只是次数不同。
例2.用计算器求![]()
解:用计算器求![]() 的步骤如下:
的步骤如下:
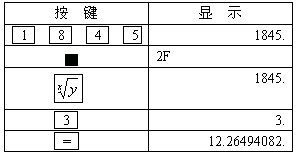
![]()
![]() ≈12.26
≈12.26
小结:由于计算器的结果较精确小数的位数较多,在遇到开方开不尽的情况下,如无特殊说明,计算结果一律保留四个有效数字。
练习:求下列各式的值
(1)![]() ; (2)
; (2) ![]() ; (3)
; (3) ![]() ; (4)
; (4) ![]()
(5) ![]() (6)
(6) ![]() (7)
(7) ![]()
(8) ![]() (9)
(9)![]() (10)
(10)![]()
例3.求下列各式中x的值(精确到0.01)
(1)![]()
解:![]()
![]()
用计算器求![]() 的值:
的值:
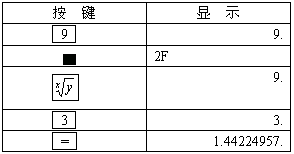
![]()
![]()
(2)![]()
解:![]()
![]()
用计算器求![]() 的值:
的值:
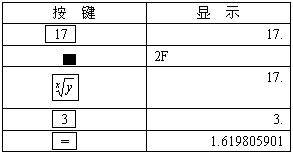
![]()
![]()
六.总结
今天学习了用计算器求一个数的立方根,求立方根的方法与平方根的方法类似,但要注意开方次数。做题要细心仔细,严格按照步骤操作。
七.作业
![]() A组1、2、3
A组1、2、3
八.板书
