第六节 平面向量的数量积及运算律

教学设计示例（第一课时）

一、教学目标

　　1．正确理解平面向量的数量积的概念，能够运用这一概念求两个向量的数量积，并能根据条件逆用等式求向量的夹角；

　　2．掌握平面向量的数量积的重要性质，并能运用这些性质解决有关问题；

　　3．通过平面向量的数量积的重要性质猜想与证明，培养学生的探索精神和严谨的科学态度以及实际动手能力；

　　4．通过平面向量的数量积的概念，几何意义，性质的应用，培养学生的应用意识.

二、教学重点  平面向量的数量积概念、性质及其应用

　　教学难点  平面向量的数量积的概念，平面向量的数量积的重要性质的理解．

三、教学具准备

　　直尺，投影仪

四、教学过程

　　1．设置情境

　　师：我们学过功的概念：即一个物体在力 的作用下产生位移 ，那么力 所做的功： ，其中 表示一个什么角度？

　　表示力 的方向与位移 的方向的夹角．

　　我们对上述物理意义下的“功”概念进行抽象，就一般向量 、 ，来规定 的含义。

　　2．探索研究

　　（l）已知两个非零向量 和 ，在平面上任取一点 ，作 ， ，则 叫做向量 与 的夹角．你能指出下列图中两向量的夹角吗？

　　① 与 的夹角为 ，② 与 的夹角为 ，③ 与 的夹角是 ，④ 与 的夹角是 ．

　　（2）下面给出数量积定义：

　　师：（板书）已知两个非零向量 和 ，它们的夹角为 ，我们把数量 ，叫做向量 与 的数量积或（内积）记作 即

　　并规定

　　师：在平面向量的数量积的定义中，它与两个向量的加减法有什么本质区别．

　　生：向量的数量积结果是一个数量，而向量的加法和减法的结果还是一个向量．

　　师：你能从图中作出 的几何图形吗？ 表示的几何意义是什么？

　　生：如图，过 的终点 作 的垂线段 ，垂足为 ，则由直角三角形的性质得：

　　所以 叫做向量 在向量 上的投影， 叫做 在 上的投影．

　　师：因此我们得到 的几何意义：向量 与 的数量积 等于 的长度 与 在 的方向上的投影 的积．

　　注意：1°投影也是一个数量，不是向量。

　　　　　2°当q为锐角时投影为正值；

　　当q为钝角时投影为负值；

　　当q为直角时投影为0；

　　当q = 0°时投影为 |b|；

　　当q = 180°时投影为 -|b|。

　　向量的数量积的几何意义：

　　数量积a×b等于a的长度与b在a方向上投影|b|cosq的乘积。

　　（3）下面讨论数量积的性质：

　　（每写一条让学生动手证一条）设 ， 都是非零向量， 是与 的方向相同的单位向量， 是 与 的夹角，则

　　①

　　②

　　③当 与 同向时， ，当 与 反向时， 。

　　特别地

　　④

　　⑤

　　3．演练反馈（投影）

　　（通过练习熟练掌握性质）

　　判断下列各题是否正确

　　（1）若 ，则对任意向量 ，有    （    ）

　　（2）若 ，则对任意非零量 ，有 （    ）

　　（3）若 ，且 ，则           （    ）

　　（4）若 ，则 或             （    ）

　　（5）对任意向量 有                  （    ）

　　（6）若 ，且 ，则          （   ）

参考答案：（l）√，（2）×，（3）×，（4）×，（5）√，（6）×．

　　4．总结提炼

　　（l）向量的数量的物理模型是力的做功．

　　（2） 的结果是个实数（标量）

　　（3）利用 ，可以求两向量夹角，尤其是判定垂直。

　　（4）二向量夹角范围 ．

　　（5）五条属性要掌握．

五、板书设计

课题 1．“功”的抽象 2．数量积的定义 3．（5）条性质 （1） （2） （3） （4） （5）

4．演练反馈 5．总结提炼

教学设计示例（第二课时）

一、教学目标

　　1．掌握平面向量的数量积的运算律，并能运用运算律解决有关问题；

　　2．掌握向量垂直的充要条件，根据两个向量的数量积为零证明两个向量垂直；由两个向量垂直确定参数的值；

　　3．了解用平面向量数量积可以处理有关长度、角度和垂直的问题；

　　4．通过平面向量的数量积的重要性质及运算律猜想与证明，培养学生的探索精神和严谨的科学态度以及实际动手能力；

　　5．通过平面向量的数量积的概念，几何意义，性质及运算律的应用，培养学生的应用意识．

二、教学重点  平面向量的数量积运算律，向量垂直的条件；

　　教学难点  平面向量的数量积的运算律，以及平面向量的数量积的应用.

三、教学具准备

　　投影仪

四、教学过程

　　1．设置情境

　　上节课，我们已经给出了数量积的定义，指出了它的（5）条属性，本节课将研究数量积作为一种运算，它还满足哪些运算律？

　　2．探索研究

　　（1）师：什么叫做两个向量的数量积？

　　生： （ 与 向量的数量积等式 的模 与 在 的方向上的投影 的乘积）

　　师：向量的数量积有哪些性质？

　　生：（1）

　　　　（2）

　　　　（3）

　　　　（4）

　　　　（5）

　　　　（6）

　　师：向量的数量积满足哪些运算律？

　　生（由学生验证得出）

　　交换律：

　　　　　

　　分配律：

　　师：这个式子 成立吗？（由学生自己验证）

　　生： ，因为 表示一个与 共线的向量，而 表示一个与 共线的向量，而 与 一般并不共线，所以，向量的内积不存在结合律。

　　（2）例题分析

　　【例1】求证：

　　（1）

　　（2）

　　分析：本例与多项式乘法形式完全一样。

　　证：         

　　注： （其中 、 为向量）

　　答：一般不成立。

　　【例2】已知 ， ， 与 的夹角为 ，求 .

　　解：∵

　　　　

　　　　

　　注：与多项式求值一样，先化简，再代入求值.

　　【例3】已知 ， 且 与 不共线，当且仅当 为何值时，向量 与 互相垂直．

　　分析：师：两个向量垂直的充要条件是什么？

　　生：

　　解： 与 互相垂直的充要条件是

　　

　　即

　　∵   

　　∴

　　∴ 

　　∴  当且仅当 时， 与 互相垂直．

　　3．演练反馈（投影）

　　（1）已知 ， 为非零向量， 与 互相垂直， 与 互相垂直，求 与 的夹角．

　　（2） ， 为非零向量，当 的模取最小值时，

　　①求 的值；

　　②求证： 与 垂直．

　　（3）证明：直径所对的圆周角为直角．

参考答案：

　　（1）

　　（2）解答：①由

　　当 时 最小；

　　②∵

　　　

　　∴ 与 垂直.

　　（3）如图所示，设 ， ， （其中 为圆心， 为直径， 为圆周上任一点）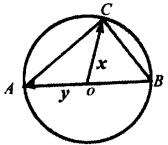

　　则

　　∵  ，

　　

　　∴   即  圆周角

　　4．总结提炼

　　（l）

　　（2）向量运算不能照搬实数运算律，如结合律数量积运算就不成立．

　　（3）要学会把几何元素向量化，这是用向量法证几何问题的先决条件．

　　（4）对向量式不能随便约分，因为没有这条运算律．

五、板书设计

课题： 1．数量积性质 2．数量积运算律

例题 1 2 3

演练反馈 总结提炼