 设为首页
设为首页
 加入收藏
加入收藏
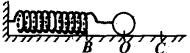
例1 如图所示,为一弹簧振子,O为振动的平衡位置,将振子拉到位置C从静止释放,振子在BC间往复运动.已知BC间的距离为20cm,振子在4秒钟内振动了10次.
(1)求振幅、周期和频率
(2)若规定从O到C的方向为正方向,试分析振子在从![]() 过程中所受回复力F,加速度a和速度v的变化情况.
过程中所受回复力F,加速度a和速度v的变化情况.
出题目的:考察弹簧振子振动中各物理量的掌握情况.
解 :(1)![]()
(2)按题设从![]() 为正方向,则当振子在平衡位置右侧时位移为正,在平衡位置左侧时位移为负.所以当振子从
为正方向,则当振子在平衡位置右侧时位移为正,在平衡位置左侧时位移为负.所以当振子从![]() 运动时,位移方向为正,大小在减少,回复力方向为负,加速度方向为负,回复力和加速度的大小都在减小.振子的速度方向为负,加速度与速度方向一致,速度在增大;振子到达O位置时位移
运动时,位移方向为正,大小在减少,回复力方向为负,加速度方向为负,回复力和加速度的大小都在减小.振子的速度方向为负,加速度与速度方向一致,速度在增大;振子到达O位置时位移![]() ,F、a均为零,v最大.当振子从
,F、a均为零,v最大.当振子从![]() 运动时,位移方向为负,位移x在增大,回复力F、加速度a方向为正,大小在增大,此过程速度方向为负,a与v反向,振子从
运动时,位移方向为负,位移x在增大,回复力F、加速度a方向为正,大小在增大,此过程速度方向为负,a与v反向,振子从![]() 做减速运动,v在减小,到达B位置时F、a为正向最大,
做减速运动,v在减小,到达B位置时F、a为正向最大,![]() .
.
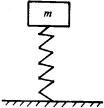
例2 如图所示,质量为m的木块放在竖直的弹簧上,m在竖直方向做简谐振动,当振幅为A时,物体对弹簧的压力最小值为物体自重的0.5倍,则物体对弹簧压力的最大值为 ,欲使物体在振动中不离开弹簧,其振幅不能超过 .
出题目的:考察回复力与振幅的理解
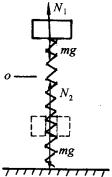
解: 物体m放在弹簧上让其缓慢下落,当重力mg与弹簧力kx相等时,物体处于平衡.在此位置对物体施加向下的压力,使物体下移位移A时,撤去外力F,物体m将在竖直方向做简谐振动.在振动过程中物体受重力和弹力作用,当压缩最小时,物体和弹簧的相互作用最小,应在平衡位置上方;当压缩量最大时,物体和弹簧的相互作用力最大,此位置应在平衡位置下方,且最小作用力和最大作用力的位置关于O点对称,离开平衡位置的距离均为A.
如图所示,物体m在最高点时弹力为,最低点时弹力为,则
![]() ①
①
![]() ②
②
由①、②式联立解得
![]()
由牛顿第三定律知
![]()
即物体对弹簧的最大压力为1.5 mg.
若要m在振动过程中不脱离弹簧,则物体m与弹簧的相互作用力达最小,即![]() ,所以最大振幅即为物体m平衡时的压缩量.
,所以最大振幅即为物体m平衡时的压缩量.
设m能达到的最大振幅为![]() ,则
,则
![]() ③
③
由①、③式联立得
![]()
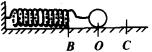
例3 一个弹簧振子的振动频率为![]() Hz,如图,振子在BC间往复运动,BC间距为20cm从振子经过平衡位置向右运动开始计时,到
Hz,如图,振子在BC间往复运动,BC间距为20cm从振子经过平衡位置向右运动开始计时,到![]() s时,振子的位移是多大?(规定向右为正方向)振子通过的路程是多少?
s时,振子的位移是多大?(规定向右为正方向)振子通过的路程是多少?
出题目的:考察对振子位移知识的掌握.
解: 由![]() Hz,可求出
Hz,可求出![]() s,由
s,由![]() cm,可知
cm,可知![]() cm.由
cm.由![]() s,可知在这段时间内振子完成全振动的次数为
s,可知在这段时间内振子完成全振动的次数为![]() ,即振子从0开始振动了16个周期另加
,即振子从0开始振动了16个周期另加![]() ,所以
,所以![]() s时振子的位移
s时振子的位移![]() cm,即振子在C位置.振子通过的路程
cm,即振子在C位置.振子通过的路程![]() .
.
例4 一弹簧振子做简谐运动,周期为T( )
A.若t时刻和![]() 时刻振子运动位移大小相等、方向相同,则
时刻振子运动位移大小相等、方向相同,则![]() 一定等于T的整数倍
一定等于T的整数倍
B.若t时刻和![]() 时刻振子运动速度的大小相等、方向相反,则
时刻振子运动速度的大小相等、方向相反,则![]() 一定等于
一定等于![]() 的整数倍
的整数倍
C.若![]() ,则在t时刻和
,则在t时刻和![]() 时刻振子运动的加速度一定相等
时刻振子运动的加速度一定相等
D.若![]() ,则在t时刻和
,则在t时刻和![]() 时刻弹簧的长度一定相等
时刻弹簧的长度一定相等
出题目的:考察对简谐运动周期的理解.
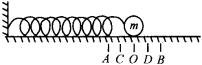
分析:如图所示,设弹簧振子以O为平衡位置,在A、B之间做简谐运动,只要t时刻与![]() 时刻振子经过同一点,则振子运动的位移(相对于平衡位置O)的大小相等、方向相同,不一定需要
时刻振子经过同一点,则振子运动的位移(相对于平衡位置O)的大小相等、方向相同,不一定需要![]() 和t的整数倍,比如振子从C→A→C,所需时间
和t的整数倍,比如振子从C→A→C,所需时间![]() ,A错,同理,振子从C→A→C,先后经过点时速度大小相等、方向相反,
,A错,同理,振子从C→A→C,先后经过点时速度大小相等、方向相反,![]() 可以小于
可以小于![]() ,B错.若
,B错.若![]() ,则在t时刻和
,则在t时刻和![]() 时刻,振子离开平衡位置的位移一定相同,因而加速度一定相同,C对,弹簧长度相等时即振子位于同一点,振子对平衡位置位移相同.
时刻,振子离开平衡位置的位移一定相同,因而加速度一定相同,C对,弹簧长度相等时即振子位于同一点,振子对平衡位置位移相同.![]() 时,不一定能满足,比如从
时,不一定能满足,比如从![]() ,但弹簧长度并不相等,D错.当然也有相等的时候,比如从
,但弹簧长度并不相等,D错.当然也有相等的时候,比如从![]() ,弹簧长度恰好相等.所以本题正确选项是C.
,弹簧长度恰好相等.所以本题正确选项是C.
点评:弹簧振子做简谐运动过程中,一个周期内在平衡位置同侧有两个时刻在同一位置,即位移大小相等、方向相同的点有两个.所以经过![]() 时间不一定就在整个周期或半个周期.
时间不一定就在整个周期或半个周期.
为了形象直观,做此类题时最好画出其示意图,以便更好地分析.